Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 135

135- O suporte em ângulo está soldado a extremidade C da viga em I e sustenta uma força vertical de 1.6   k N . Determine o momento fletor em B e a distância x a esquerda de C na qual o momento fletor vale zero. Construa também o diagrama de momento para a viga.

Passo 1

Considerando as reações positivas em A e B nós teremos a somatória das forças verticais iguais a zero:

R a + R b = 1.6   k N

E para o momento não podemos afirmar muita coisa por essa força de 1.6   k N por conta desse braço, só podemos afirmar que em C temos o momento igual a:

M = - 1.6 k N × 200 × 10 - 3 = - 320   N m

E por causa desse momento nós podemos transferir a força para o ponto C da seguinte forma:

Já que estaremos consideram o sentido horário como o positivo.

Logo a somatória dos momentos em A será:

- R b × 400 × 10 - 3 - 320 + 1.6 k N × 850 × 10 - 3 = 0 → R b = 2600 N

Logo R a será:

R a = 1600 - 2600 = - 1000   N

Passo 2

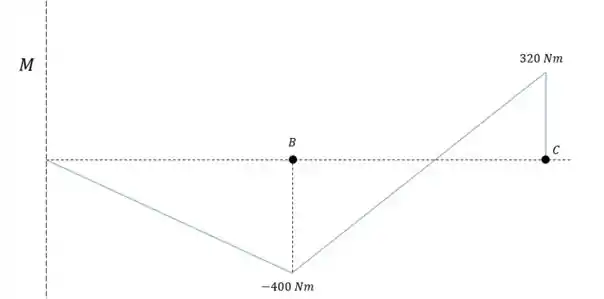
Fazendo o momento fletor no intervalo de 0   a   400   m m nós teremos a seguinte seção da barra.

Calculando o momento em relação ao ponto mais extremo a direita teremos um momento igual a:

- 1000 × x - M = 0

M = - 1000 x

O que nos dá um momento em x = 400   m m igual a M = - 1000 × 0.4 = - 400   N m

Agora para o intervalo de 400   m m   a   850   m m .

A cortante resultante no ponto B será o - 1000 da reação A somado com os 2600 da reação B o que dá 1600   N , junto com o momento resultante da seção anterior. Teremos a seção equivalente da figura abaixo.

Se somarmos os momentos no ponto mais a direita da seção teremos:

- 400 + 1600 × x - 0.4 - M = 0

M = 1600 x - 1040

Onde para x = 0.85 teremos um momento resultante de 320   N m que se anula com o momento existente no braço.

Resposta

M b = - 400   N m

Diagrama do momento fletor:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a curva de deflexão do cabo discutido no Exemplo 7.13 se reduz à equação 4 no exemplo 7.12 quando a função de cosseno hiperbólico é expandida em termos de uma série e apenas os dois primeir
Se a força de reboque horizontal for T = 20k N e a corrente tem uma massa por unidade de comprimento de 15k g / m , determine a flecha máxima h . Despreze o efeito da flutuação da água sobre a corrent
Se h = 5m , determine a tração máxima desenvolvida na corrente e seu comprimento, a corrente tem uma massa por unidade de comprimento de 8k g / m .
Se o cabo de 45m de comprimento tem uma massa por unidade de comprimento de 5k g / m , determine a equação da curva catenária do cabo e a tração máxima desenvolvida no cabo.
O tabuleiro da ponte tem um peso por unidade de comprimento de 80k N / m . Ele está apoiado em cada lado por um cabo. Determine a tração em cada cabo nos pilares A e B .