130- Desenhe os diagramas de cortante e de momento para a viga em balanço carregada, para a qual o momento é ajustado de modo a produzir um momento nulo na extremidade engastada da viga. Determine o momento fletor em .

O que faz com que a nossa viga tenha uma equivalência igual a:

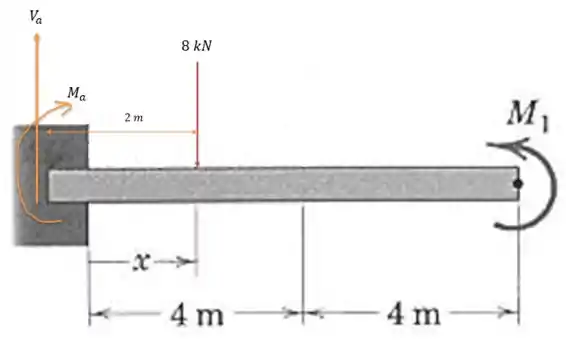
Isso faz com que o cortante em seja:

E a questão nos diz que seja zero, logo se fizermos a somatória dos momentos em seja:

Desenhando a viga de modo a obtermos o valor da cortante e do momento fletor no intervalo de :

A cortante dessa viga se encontra fazendo a somatória das forças verticais, que é:

Uma vez que a equação da carga é igual a:

Pois independente do valor de o valor de sempre será .

Logo em o nosso cortante será .

Agora o momento nessa viga será:

Onde no ponto de temos um momento igual a:

E em temos um valor de momento igual a:

Agora na seção de :

Fazendo a somatória das forças verticais temos:

E a somatória dos momentos:

Porém como o valor de também é de porém no sentido contrário então temos em um começo igual a e termina com o valor de .