Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 148

137- Repita o Prob. 5/136 substituindo a carga de 1500   N pelo momento de 4.2   k N m

Passo 1

Assim como na questão anterior a carga retangular aplica na nossa viga uma força resultante de 2400   N na posição de 3.5   m . O que faz com que nossa viga equivalente fique da seguinte maneira.

Logo a somatória das forças horizontais será:

R a + R b = 2400   N

E a somatória dos momentos em A (considerando que o sentido horário é positivo)

2400 × 3.5 + 4200 - R b × 9 = 0 → R b = 1400   N

Logo R a será:

R a = 2400 - 1400 = 1000   N

Passo 2

Analisando a viga no intervalo de 0 < x < 2 :

Fazendo a somatória das forças verticais encontramos:

V = 1000   N

Para toda a seção.

E para o momento nós encontramos:

M = 1000 x

Para o extremo da seção temos um momento de:

M = 1000 × 2 = 2000 N m

Passo 3

Agora para 2 < x < 5 :

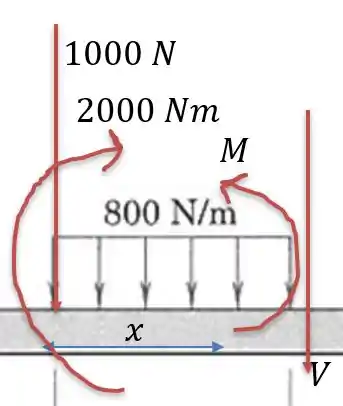
Somando as componentes verticais temos a cortante:

1000 - 800 ( x - 2 ) = V

Logo nossa equação de cortante será:

V = 2600 - 800 x

Logo para x = 5 a cortante será:

V = 2600 - 800 × 5 = - 1400   N

E para encontrar o momento fazemos o seguinte:

M = 2000 + 1000 x - 2 - 800 2 ( x - 2 ) ( x - 2 )

M = 2000 + 1000 x - 2000 - 400 ( x 2 - 4 x + 4 )

M = 1000 x - 400 x 2 + 1600 x - 1600 = - 400 x 2 + 2600 x - 1600

Pra x = 5 temos o momento:

M = - 400 × 25 + 2600 × 5 - 1600 = 1400

Passo 4

Para o intervalo 5 < x < 7 :

A somatória da cortante é:

V = - 1400   N

A somatória dos momentos dá:

M = 1400 - 1400 x - 5 → - 1400 x + 8400

Logo para x = 6 temos um momento em:

M = - 1400 × 6 + 8400 = 0   N m

Para x = 7 temos um momento final igual a:

M = - 1400 N m

Porém como temos um momento que adiciona 4200   N m ao sistema temos um salto de - 1400   N m até:

M = - 1400 + 4200 = 2800   N m

Passo 5

Agora para o intervalo de 7 < x < 9 :

Nossa cortante continua:

V = - 1400   N

Agora para o momento:

M = 2800 - 1400 ( x - 7 )

M = - 1400 x + 12600

E para x = 9 temos:

M = - 1400 × 9 + 12600 = 0

O que prova que estamos certos.

Passo 6

No passo 4 encontramos um momento de 2800   N m mas não podemos cravar ainda que esse momento é o maior da viga, pois temos no passo 3 uma parábola que tem um máximo local entre 2 e 5. Vamos derivar a equação do momento e ver a posição do seu maior valor.

d d x - 400 x 2 + 2600 x - 1600 = 0

- 800 x + 2600 = 0 → x = 3.25

Logo em x = 3.25   m teremos um momento de :

M = - 400 × 3.25 2 + 2600 × 3.25 - 1600 = 2625   N m

Logo o maior momento realmente é de 2800   N m em x = 7

Resposta

M _ max ⁡ = 2800 N m

Em x = 6 :

V = - 1400   N m

M = 0   N m

Diagrama de cortante:

Diagrama do momento fletor:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine o esforço cortante e o momento fletor como uma função de x , onde 0 ≤ x3m e 3m ≤ x ≤ 6m , e depois contrua os diagramas de esforço cortante e de momento fletor.
Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine a força normal, a força cortante e o momento fletor interno nos pontos DeE da estrutura.
Determine a força normal, a força cortante e o momento fletor interno como uma função de 0 ° ≤ θ ≤ 180 ° e 0 ≤ y ≤ 0,6 m para o membro carregado conforme mostrado.