Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 18

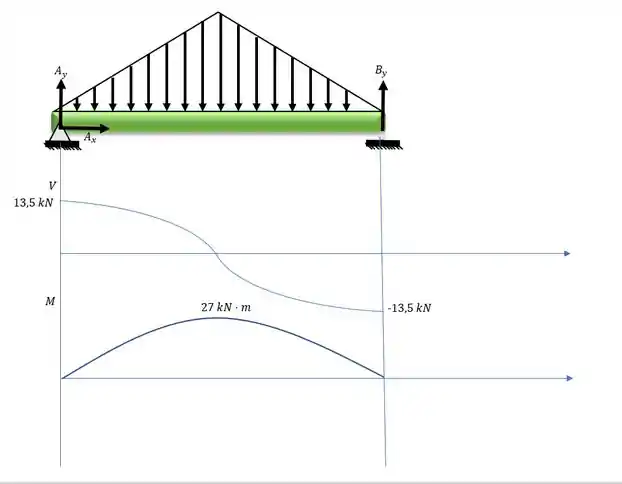
Determine os diagramas de esforço cortante e de momento fletor para a viga.

Passo 1

Desenhando o diagrama de corpo livre:

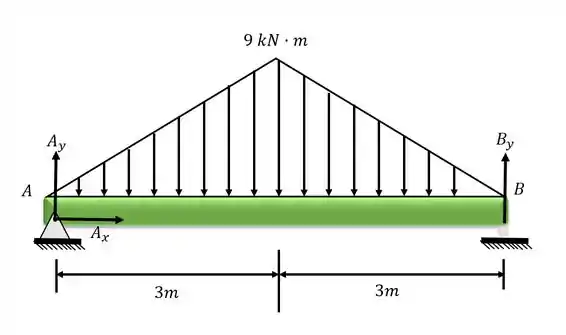
Passo 2

Com o diagrama do corpo livre, podemos calcular as reações de apoio

∑ F y = 0 A y + B y = 2 × 1 2 ⋅ 9 × 3 = 27   k N

Lembrando que a força resultante de um carregamento triangular é dada por: 1 2 w x

Como o carregamento é simétrico, A y = B y = 27 2 = 13,5   k N

Passo 3

Analisando o trecho de 0 ≤ 3 m :

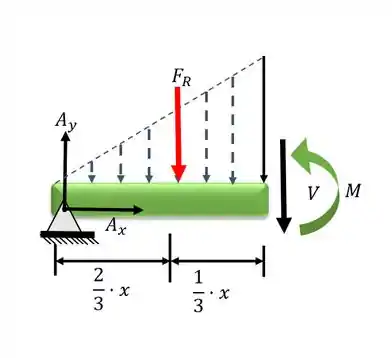
Utilizando as equações do equilíbrio no eixo y e do momento no eixo seccionado:

∑ F y = 0 V - A y + F R = 0 V - 13,5 + 1 2 × 9 × x = 0 V = 13,5 - 4,5 x ∑ M   = 0 M + F R × 1 3 x - 13,5 x = 0 M = - F R × 1 3 x + 13,5 x M = - 1 2 9 x × 1 3 x + 13,5 x M = - 1,5 x 2 + 13,5 x

Analisando o trecho de 6 ≤ x ≤ 9   m :

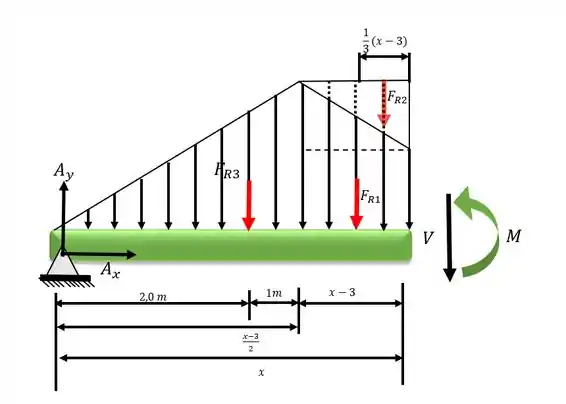
Utilizando as equações do equilíbrio no eixo y e do momento no eixo seccionado:* Utilizar um carregamento triangular fictício para não ter que integrar

* Substituir os carregamentos distribuídos por forças resultantes equivalentes F R 1 , F R 2 , F R 3 atuantes no centro de massa do triângulo e dos retângulos.*Lembrar que o centro de massa do triângulo fica a 1/3 da base F R 2 = 1 2 w x = - 1 2 × 9 × ( x - 3 )

∑ F y = 0 V - A y + F R 1 + F R 2 = 0 V - 13,5 + 9 x - 3 - 1 2 × ( 9 ) × x - 3 = 0 V = 13,5 + 9 x - 27 - 4,5 x + 27 V = 13,5 - 4,5 x

∑ M   = 0 M + F R 1 × x - 3 2 + F R 2 × 2 3 x - 3 - 13,5 x + F R 3 × x - 3 + 1 = 0 M + 9 x - 3 × x - 3 2 + - 1 2 × 9 × x - 3 × 1 3 x - 3 - 13,5 × x   + 1 2 × 9 × 3 × x - 2 = 0 M + 4,5 x 2 - 6 x + 9 - 1,5 x 2 - 6 x + 9 - 13,5 x + 13,5 x - 27 = 0 M = 3 x 2 - 6 x + 9 - 27 = 0 M = 3 x 2 - 18 x + 27 - 27 = 0 M = 3 x 2 - 18 x

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo A B está sujeito a uma carga uniforme de 200 N/m. Se o peso do cabo for desconsiderado e os ângulos de inclinação nos pontos A e B forem 30 ° e 60 ° , respectivamente, determine a curva que def
Determine a força normal, a força cortante e o momento fletor nos pontos D e E .
Determine os diagramas de força cortante e de momento fletor para a viga
Se o cilindro E tem massa de 20 kg e cada segmento do cabo pode sustentar uma tração máxima de 400 N, determine a maior massa do cilindro F que pode ser suportada. Além disso, qual é a flecha y C ?
Se os cilindros E e F têm massa de 20 kg e 40 kg, respectivamente, determine a tração desenvolvida em cada cabo e a flecha y C .