Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 100
93- Calcule a massa de concreto necessária para construir a represa em arco mostrada. O concreto tem uma massa específica de
Passo 1
Pense nessa represa vista de cima, tal como na figura abaixo:
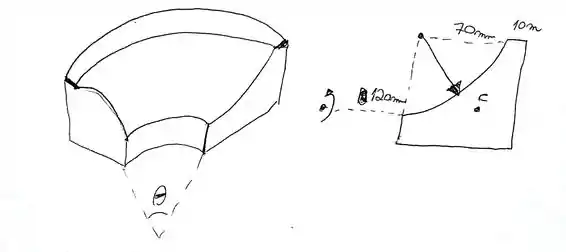
E seu volume é calculado da seguinte forma:
Onde é o ângulo que essa imagem é rotacionado, é o centroide nesse raio de rotação, sua área.
Passo 2
Calculando a área dessa figura basta calcular a área do quadrado e diminuir a área do quarto de círculo.
Para calcular o centroide basta fazer:
O numerador é a multiplicação do centroide da figura com a área dessa figura, e que assim como o cálculo da área basta fazer essa conta do quadrado e diminuir da do círculo.
Calculando então o centroide:
Passo 3
O volume formado por essa região será:
E como sua densidade é nós teremos:
Como encontramos o volume, logo nossa massa será: