Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 139

139- Determine as forças nos elementos A D e D G .

Passo 1

Para resolver essa questão nós precisamos de bastante entendimento do método das seções pois vamos precisar cortar mais dos que as três barras recomendadas pelo método. Para encontrar a força na barra G D , F D C F , B F , D E e B E . Só que invés de fazer a somatória dos momentos em um ponto específico vamos fazer a somatória em um eixo. Mas primeiro vamos fazer o desenho disso.

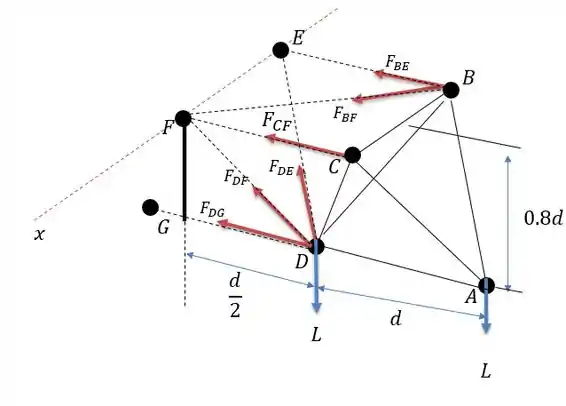
As forças F_D F , F_D E , F_C F , F_B F e F_B E apontam para o eixo x logo eles não geram momento.

É como se você fizesse uma força num eixo de uma porta, não importa a inclinação você nunca moverá a porta. A ideia aqui é a mesma.

Logo fazendo o somatório dos momentos em x nós teremos:

F_D G xx 0.8 d + L xx (d)/(2) + L xx (d + (d)/(2)) = 0

0.8 d F_D G = - (L d)/(2) - (3 L d)/(2)

F_D G = - (2 L d)/(0.8 d) = - 2.5 L = 2.5 L C

Surpreendente né.

Passo 2

A mesma coisa pode ser feita para a força em A D .

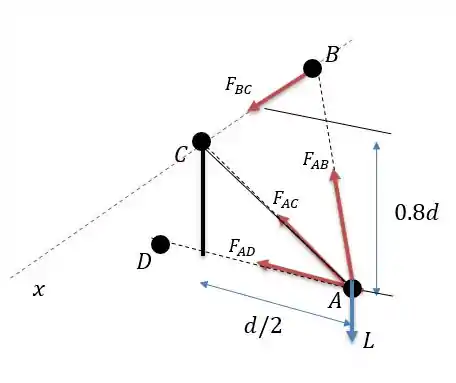
Da mesma forma as forças F_A C , F_A B e F_B C apontam para o eixo x e por isso elas não geram momento em x , logo o momento no eixo x será:

F_A D xx 0.8 d + L xx (d)/(2) = 0

F_A D = - (d L)/(2 xx 0.8 d) = - 0.625 L = 0.625 L C

Resposta

F_D G = 2.5 L C

F_A D = 0.625 L C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A estrutura representada está sendo considerada como a parte superior de uma torre de linha de transmissão e é apoiada nos pontos F, G, H e I. O ponto C está diretamente acima do centro do retângulo F
Determine as forças nos membros AC e BD da treliça piramidal invertida com base retangular. O ponto M é o ponto médio de BD.
A treliça espacial de Prob. 4/63 é modificado conforme mostrado em que seus suportes e carregamento são alterados. Determine as forças nas barras AC e BD e compare com os resultados do Prob. 4/63.
Para a treliça espacial mostrada, verifique a suficiência dos apoios e também a quantidade e disposição das barras para garantir a determinação estática, tanto externa quanto interna. Por inspeção, de
Cada um dos pontos de apoio B, C, D, E e F é considerado como tendo um contato simples e sem atrito com a superfície de apoio horizontal. Para a carga vertical L mostrada, quais seriam as forças em to