143- O tipo de guindaste marítimo mostrado é usado tanto para operações nas docas quanto embarcado. Determine a força no elemento , faça seu gráfico em função do ângulo do mastro para e calcule o valor dessa força para . Despreze o raio de todas as polias e o peso do mastro.
Passo 1
Para resolver esse exercício precisamos ir decompondo a força exercida pela caixa até chegar no elemento que queremos chegar. Literalmente ir decompondo a força da direita para esquerda. Redesenhando esse desenho com as forças no cabo de tração do guindaste nós teremos:
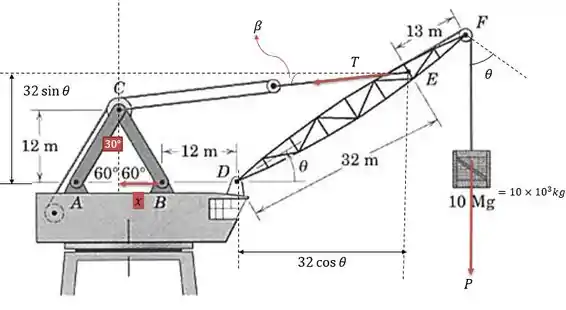
Para sermos capazes de encontrar a força do cabo da figura acima nós precisamos encontrar o valor de em função de , rebater as forças e fazer a somatória dos momentos em .
O valor de é a tangente formada pelos comprimentos:
Cateto oposto:
Cateto adjacente:
Onde é a metade da base do triângulo isósceles .
Logo o valor de será:
Passo 2
Agora que está em função de nós podemos calcular os momentos em relação a , para podemos encontrar a força que nos levará ao seu suporte.
Onde o peso da caixa é calculado por:
A melhor ideia é rebater o guindaste em e assim como a força em e de modo que temos a figura abaixo equivalente a desse guindaste.
Logo o valor de ao fazer a somatória dos momentos em ser nula nos dá:
Onde deixamos o valor de positivo de modo a considerar que a sua reação também irá sair do nó.
Passo 3
Agora essa força é transmitida para a polia. De modo que temos o seguinte sistema de forças.
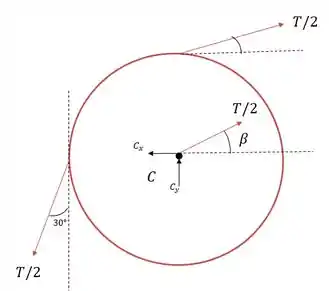
Já que a força de tração é dividida ente dois cabos igualmente e transmitida para o pino que possui as duas reações.
Logo fazendo a somatória na vertical nós teremos:
Logo:
Agora a somatória das forças na horizontal nos dá:
O que dá:
Passo 4
Agora finalmente seremos capazes de descobrir a força na barra ao utilizar as forças no pino para as duas barras de suporte que vem logo abaixo ao analisar justamente a somatória no pino .
Para o sistema ficar estático devemos considerar que as reações em seja contrárias ao do sistema anterior.
Logo fazendo a somatória das forças horizontais temos:
E a somatória das forças verticais nos dá:
Se arrumarmos a primeira equação teremos:
Trocando o sinal:
E arrumando a segunda equação.
Somando essas duas equações encontraremos a força na barra :
Agora todos os elementos estão conectados matematicamente, sendo possível plotar o gráfico.
Resposta
Gráfico:
Medida de em .
Link pro gráfico: https://www.desmos.com/calculator/gjcl7n1gnh
Para ,