141- Um cabo pesado, com massa de por metro de comprimento, passa sobre os dois tubos presos distantes entre si, e em um mesmo nível. Uma extremidade sustenta um cilindro de . Experimentalmente determina-se que uma força de direcionada para baixo é necessária para induzir escorregamento do cabo sobre ambos os tubos a uma taxa constante. Determine o coeficiente de atrito dinâmico entre o cabo e os tubos, a força trativa máxima no cabo entre os tubos e a deflexão no cabo.
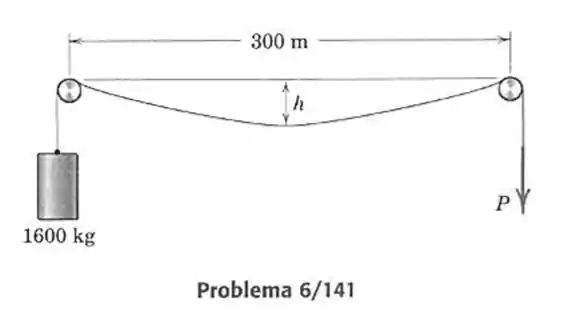
Passo 1
O cabo faz um ângulo de abraçamento desconhecido e que pode ser escrito como:
por que as duas forças (a do peso e a força ) apontam para baixo e devido a catenária formada pelo cabo pesado que tem um peso específico igual a:
Passo 2
A força de tração na extremidade do cabo com a polia pode ser representado da seguinte forma:
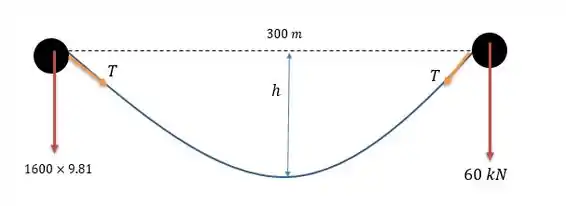
Considerando que a força seja uma força que encontra-se entre os valores de e temos o seguinte sistema para resolver. (equação de trações em uma polia com atrito).
Com esse valor de tração conseguimos encontrar , substituindo na primeira equação:
Tirando o log neperiano encontramos:
Passo 3
Agora podemos encontrar a força de tração no meio da corda pela equação:
Resolvendo numericamente encontramos um valor próximo a:
Com o valor de conseguimos encontrar o valor inicial de , pela equação:
Então o atrito na polia será de:
Passo 4
Agora a deflexão se dará pela equação:
Substituindo os valores que conhecemos:
Uma baita de uma deflexão!