Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 231

O corpo afilado tem uma seção transversal horizontal circular. Determine a altura h - de seu centro de massa, acima da base do sólido homogêneo.

Passo 1

A fórmula da coordenada z - do centro de massa de um corpo sólido homogêneo é:

z - = ∫ z   d V ∫ d V

Então devemos resolver as duas integrais e acharemos o valor de h - .

Passo 2

Primeiro vamos calcular o volume V = ∫ d V . Vamos relacionar o raio r de cada disco de espessura infinitesimal d z com a coordenada z . Olhamos um corte por um plano vertical passando pelo meio do corpo:

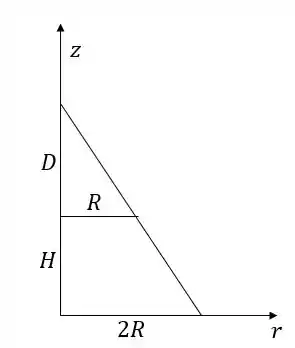
Por semelhança de triângulos, achamos o tamanho D :

D + H 2 R = D R ⇒ R D + R H = 2 R D ⇒ R D = R H ⇒ D = H

Agora se pegarmos uma altura z qualquer, calculamos o raio r ( z ) também por semelhança de triângulos:

2 H 2 R = 2 H - z r ⇒ 2 r H = 4 R H - 2 z R ⇒ r = 4 R H - 2 z R 2 H

⇒ r z = 2 R - R H z

Passo 3

Já temos o raio em função da altura, vamos então ahcar a expressão de d V para podermos integrar. O volume de um disco de espessura d z é dado por:

d V = π r 2 d z = π 2 R - R H z 2 d z = π R 2 H 2 z 2 - 4 R 2 H z + 4 R 2 d z

Então vamos integrar d V com z indo de 0   a H :

V = ∫ d V = ∫ 0 H π R 2 H 2 z 2 - 4 R 2 H z + 4 R 2 d z = π R 2 3 H 2 z 3 - 2 R 2 H z 2 + 4 R 2 z d z 0 H

= π R 2 3 H 2 H 3 - 2 R 2 H H 2 + 4 R 2 H = π R 2 H 3 - 6 R 2 H 3 + 12 R 2 H 3 = 7 3 π R 2 H

Passo 4

Agora vamos calcular ∫ z   d V :

∫ z   d V = ∫ 0 H π z R 2 H 2 z 2 - 4 R 2 H z + 4 R 2 d z = ∫ 0 H π R 2 H 2 z 3 - 4 R 2 H z 2 + 4 R 2 z d z

= π R 2 4 H 2 z 4 - 4 R 2 3 H z 3 + 2 R 2 z 2 0 H = π R 2 4 H 2 H 4 - 4 R 2 3 H H 3 + 2 R 2 H 2

= π 3 R 2 H 2 12 - 16 R 2 H 2 12 + 24 R 2 H 2 12 = 11 12 π R 2 H 2

Passo 5

Só falta dividir as duas integrais e chegamos no resultado:

h - = z - = ∫ z   d V ∫ d V = 11 12 π R 2 H 2 7 3 π R 2 H = 11 12 ⋅ 3 7 H = 11 28 H

Resposta

h - = 11 28 H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a coordenada x do centro de massa da parte da casca esférica, que tem espessura uniforme, mas fina.
Determine as coordenadas x e y do centroide da área sombreada.
Determine a coordenada x do centro de massa do hemisfério homogêneo, que teve removida a região hemisférica menor.
Determine a coordenada y do centroide da área plana mostrada. Coloque h = 0 em seu resultado e compare-o com o resultado y - = 4 α 3 π para área semicircular (veja o Exemplo 5/3 e a Tabela D/3). Avali
Determine a coordenada x do centro de massa do corpo sólido homogêneo mostrado.