Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 96

O empuxo hemisférico que se sustenta no final do eixo suporta uma força axial P . Derive a expressão para o momento M necessário para girar o eixo a velocidade constante se a pressão p for proporcional a sen ⁡ α e o coeficiente de atrito é μ .

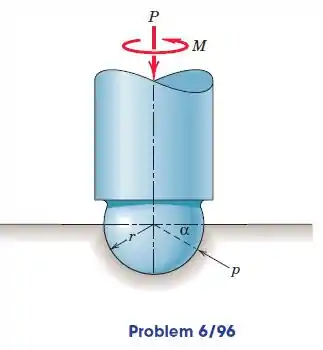
Passo 1

Precisamos encontrar uma expressão para o momento M que faz com que o eixo gire em uma velocidade constante.

Nos é dito que a pressão é proporcional a sen ⁡ α . Portanto podemos expressá-la da seguinte forma:

p = k s e n ⁡ α

Onde k é uma constante de proporcionalidade.

A equação para calcular o binário máximo M é dada por:

d M = μ p r cos ⁡ α d A

Substituindo p , temos que:

d M = μ k sen ⁡ α r cos ⁡ α d A

Passo 2

Precisamos determinar o valor de d A . Temos que um elemento da seção infinitesimal do rolamento será dado por:

d A = r d α 2 π r cos ⁡ α

d A = 2 π r 2 cos ⁡ α d α

Substituindo na equação, temos que:

d M = μ k sen ⁡ α r cos ⁡ α 2 π r 2 cos ⁡ α d α

d M = 2 π k r 3 μ sen ⁡ α cos 2 ⁡ α d α

Integrando este termo, temos que:

M = ∫ 0 π / 2 2 π k r 3 μ sen ⁡ α cos 2 ⁡ α d α

M = 2 π k r 3 μ ∫ 0 π / 2 sen ⁡ α cos 2 ⁡ α d α

Resolvendo, temos que:

M = 2 π k r 3 μ - cos 3 ⁡ α 3 0 π / 2

M = 2 3 π k r 3 μ

Passo 3

Ainda podemos expressar esta equação em termos da força P .

Sabemos que a pressão é dada pela força sobre a área. Logo:

d P = p d A

Onde P indica a força axial.

Substituindo a pressão p e integrando este termo, temos que:

P = ∫ 0 π / 2 k sen ⁡ α 2 π α r 2 cos ⁡ α d α

P = 2 π k r 2 ∫ 0 π / 2 sen ⁡ α cos ⁡ α d α

Resolvendo, temos que:

P = 2 π k r 2 sen 2 ⁡ α 3 0 π / 2

P = 2 3 π k r 2

Portanto, temos que o momento é dado por:

M = P r μ

Resposta

M = P r μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 8.90 considerando que a força normal por unidade de área entre o disco e o assoalho varia linearmente desde um máximo no centro até zero na circunferência do disco.
Um patinete é projetado para andar à velocidade constante em um declive com 2 % de inclinação. Considerando que o coeficiente de atrito cinético entre o eixo de 25m m e o mancal é 0,10 , determine o d
Sabendo que um disco de 150m m de diâmetro rola a uma velocidade constante em um declive com 2 % de inclinação, determine o coeficiente de resistência ao rolamento entre o disco e o declive.
À medida que as superficies de um eixo e um mancal desgastam-se, a resistência ao atrito de um mancal de escora diminui. Geralmente, considera-se que o desgaste é diretamente proporcional à distância
Suponto que a pressão entre as superfícies de contato seja uniforme, mostre que a intensidade M do binário necessário para se vencer a resistência de atrito para o mancal cônico mostrado é: M = 2 3 ⋅