Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 142

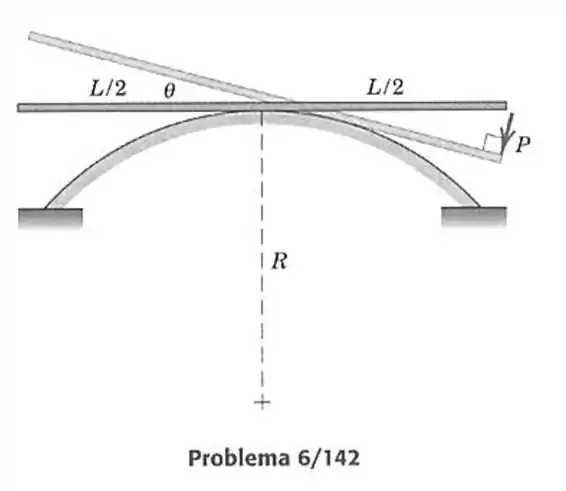
142- A barra esbelta uniforme de massa m e comprimento L está inicialmente em repouso, em uma posição horizontal centrada, sobre a superfície circular fixa de raio R = 0.6 L . Se uma força P normalmente a barra é aplicada gradualmente a sua extremidade, determine o ângulo de equilíbrio máximo θ que a barra pode atingir antes de escorregar. O coeficiente de atrito estático entre a barra e seu apoio vale 0.15 .

Passo 1

A força P faz com que o ponto de contato da barra na superfície circular esteja em uma posição adiantada a R θ da do ponto inicial, pois é o comprimento do arco percorrido pela barra, logo o sistema de forças na barra fica da seguinte maneira.

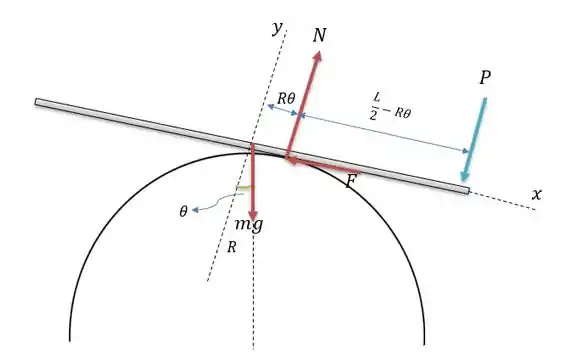
Para facilitar nossa vida é bem mais prático considerar o eixo paralelo as forças P e normal a placa.

Passo 2

Fazendo a somatória das forças verticais ser zero nós temos:

N - P - m g c o s   θ = 0

E a somatória das forças horizontais ser zero.

- F + m g sin ⁡ θ = 0 → F = m g sin ⁡ θ

Onde F = 0.15 N .

N = m g sin ⁡ θ 0.15

Substituindo esse valor de N na primeira equação nós teremos:

P = m g sin ⁡ θ 0.15 - m g cos ⁡ θ

Passo 3

Agora vamos fazer a somatória dos momentos no ponto de contato da barra com o plano.

m g R θ cos ⁡ θ = P L 2 - R θ

Como R = 0.6 L temos:

0.6 m g L θ c o s   θ = P L 2 - 0.6 P L θ

Cortando L e substituindo o valor de P temos a seguinte relação:

0.6 m g θ cos ⁡ θ = m g sin ⁡ θ 0.15 - m g cos ⁡ θ 1 2 - 0.6 θ

Cortando m g :

0.6 θ cos ⁡ θ = sin ⁡ θ 0.3 - cos ⁡ θ 2 - 4 θ sin ⁡ θ + 0.6 θ cos ⁡ θ

0 = sin ⁡ θ 1 0.3 - 4 θ - cos ⁡ θ 2

t g θ = 1 2 1 0.3 - 4 θ

t g θ = 0.3 2 - 2.4 θ

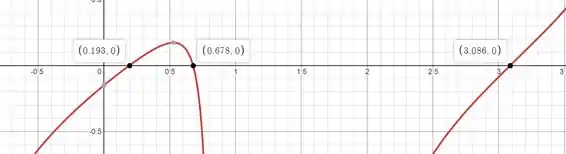
Em radianos temos os seguintes ângulos na qual a equação t g   x - 0.3 2 - 2.4 x será zero será:

θ = 0.193 r a d = 11.06 °

θ = 0.678   r a d = 38.85 °

θ = 3.086   r a d = 176.81 °

Temos que pegar o menor valor de ângulo encontrado pois depois desse valor a barra já vai ter escorregado e caído. Logo:

θ = 11.06 °

Resposta

θ = 11.06 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo homogêneo com dois pés pequenos e duas rodas ideais estão em repouso na inclinação acidentada. (a) Suponha sem derrapagem e determine o valor máximo do ângulo θ para o qual o corpo não vira em
Um carpinteiro de 100k g se agacha sobre uma folha de 18k g de contraplacado quando ele está prestes a efetuar um conserto de telhas. Determine a força de atrito que a superfície do telhado exerce sob
Repita o Prob. 6 / 28 , mas agora o carro tem roda dianteira.
A força P é aplicada a (a) o bloco de 60l b e (b) o bloco de 100l b . Para cada caso, determine omagnitude de P necessária para iniciar o movimento.
A escora AB de massa desprezível é articulada com a horizontal superfície em A e para a roda uniforme de 25 kg em B. Determine o par mínimo M aplicado a roda que fará com que ela escorregue se o coefi