Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 107

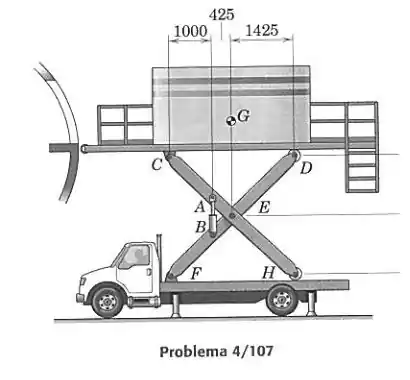
O caminhão mostrado é usado para entregar refeições para aviões. A unidade elevada tem uma massa de 1000 kg, com centro de massa em G . Determine a força necessária no cilindro hidráulico A B .

Passo 1

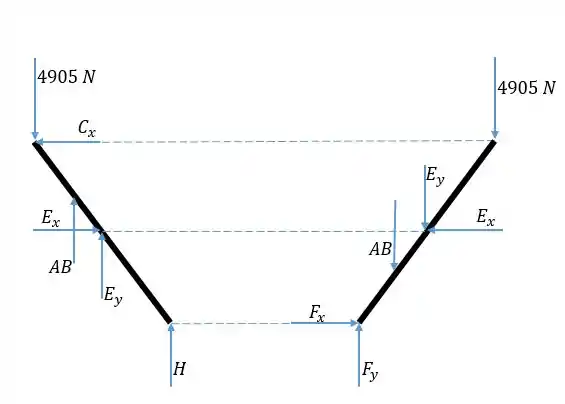
Vamos representar as barras C H e D F em diagrama de corpo livre. Pela simetria, cada barra suporta metade do peso da unidade. Então temos em C e D forças verticais de:

1000 × 9,81 2 = 4905   N

Os apoios em H e D o impedem de ter forças horizontais nesses pontos.

Passo 2

Primeiramente, olhando para as duas barras, o pino   E e A B como um todo, pela simetria temos H = F y = 4905   N . Agora devemos aplicar equações de equilíbrio para cada barra para determinar as outras forças. Vamos primeiro fazer a soma das forças em x e y e o momento em torno de E para C H :

∑ F x = 0 ⇒ C x = E x       ( 1 )

∑ F y = 0 ⇒ A B + E y + 4905 - 4905 = 0 ⇒ E y = - A B       ( 2 )

∑ M E = 0 ⇒ - A B 425 + 4905 1425 + 4905 1425 + C x 1425 = 0

⇒ 13979250 + 1425 C x - 425 A B = 0       ( 3 )

Passo 3

Agora vamos fazer as equações para a barra D F :

∑ F x = 0 ⇒ E x = F x       ( 4 )

∑ F y = 0 ⇒ E y = - A B

∑ M E = 0 ⇒ - 4905 - 4905 + F x 1425 + A B ( 425 ) = 0

⇒ - 13979250 + 1425 F x + 425   A B = 0       ( 5 )

Passo 4

Se somarmos as equações (3) e (5), temos:

13979250 + 1425 C x - 425 A B - 13979250 + 1425 F x + 425   A B = 0

⇒ 1425 C x + F x = 0 ⇒ C x + F x = 0

Mas sabemos de (1) que C x = F x , então:

2 C x = 0

C x = F x = 0

Agora pegamos (5) novamente:

- 13979250 + 1425 × 0 + 425   A B = 0

⇒ 425   A B = 13979250

⇒ A B = 13979250 425 = 32892   N ≈ 32,9   k N

Resposta

A B = 32,9   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

120- A figura mostra um dispositivo especial, projetado para levantar seções verticais de uma torre de construção. O conjunto A tem uma massa de 1.5M g e é erguido pela plataforma B , que tem uma mass
119- O mecanismo de poda de uma serra com cabo está mostrado no momento em que ele corta um galho, S . Para a posição particular mostrada, a corda de fixação é paralela ao cabo e suporta uma força de
121- Determine a força atuando no elemento A B C na conexão A para o suporte espacial carregado mostrado. Cada conexão pode ser tratada como uma rótula.
122- Na representação esquemática de uma estrutura real, T representa um parafuso de aperto, C e D são dobradiças cujos eixos estão ao longo da linha C D e B , E e F são rótulas. Determine a força de
Determine a reação no rolete F para o suporte carregado mostrado