Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 97

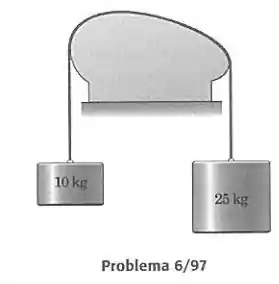
Os blocos de 10 kg e de 25 kg estão presos por uma corda pendurada sobre a superfície curva fixa. Se o sistema está no limiar de escorregar, calcule o coeficiente de atrito entre a corda e a superfície.

Passo 1

Se a corda está no limiar de escorregar, ela ainda está em equilíbrio. A fórmula para o equilíbrio de uma corda enrolada em volta de uma superfície é dada por:

ln ⁡ T 2 T 1 = μ β

Sendo T 2 e T 1 as trações maior e menor nas extremidades da corda, μ o coeficiente de atrito entre a corda e a superfície e β o ângulo total de giro da corda. Como a fórmula não envolve um raio específico, a superfície não precisa ser circular (como numa polia), e esse ângulo β nesse caso é o ângulo de meia volta, β = π . Com a fórmula, devemos achar μ .

Passo 2

A tração maior T 2 é feita pelo peso do bloco 25 kg e a tração menor T 1 pelo peso do bloco de 10 kg. Jogando então na fórmula:

ln ⁡ T 2 T 1 = μ β

⇒ ln ⁡ 25 g 10 g = π μ ⇒ μ = ln ⁡ 2,5 π = 0,292

Resposta

μ = 0,292

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de freio de automóvel consiste em um rotor de faces planas e uma pinça que tem uma sapata em cada lado do rotor. Para forças P idênticas atuando atrás de cada sapata, mostre que o momento apl
No projeto de um teste de atrito, o eixo A é frouxamente preso ao mancal da biela, que tem centro de gravidade em G , como mostrado. Com a biela inicialmente na posição vertical, o eixo é girado lenta
Para o disco de lixamento plano de raio a , a pressão p desenvolvida entre o disco e a superfície lixada decresce linearmente com r , desde um valor p 0 no centro aé p 0 / 2 com r = a . Se o coeficien
133- A figura mostra uma chave a fricção para girar a roda no sentido anti-horário sob a ação de uma força P aplicada ao cabo. O conector flutuante A B se prende a roda de forma que θ = 20 ° . Se uma
129- Determine a faixa de massas m do cilindro para a qual o sistema está em equilíbrio. O coeficiente de atrito entre o bloco de 50k g e o plano inclinado vale 0.15 e aquele entre a corda e o apoio c