Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 167

167- Uma linha de transmissão está suspensa entre duas torres distando de 200   m sobre uma mesma linha horizontal. O cabo tem uma massa de 18.2   k g por metro de comprimento e tem uma deflexão de 32   m no seu ponto médio. Se o cabo pode suportar uma força trativa máxima de 60   k N , determine a massa ρ de gelo, por metro, que pode se formar sobre o cabo sem exceder a máxima força trativa do cabo.

Passo 1

Anotando os dados da questão nós temos:

Deflexão: y = 32   m

Ponto médio do cabo x = 100   m

Tração máxima T = 60   k N

Densidade da corda: 18.2 k g m

Passo 2

Colocando esses dados na equação 5 / 19 nós temos;

32 = T 0 μ   cosh ⁡ 100 μ T 0 - 1

Agora utilizando a equação 5 / 22 nós temos:

60 × 10 3 = T 0 + 32 μ → T 0 = 60 × 10 3 - 32 μ

Substituindo T 0 na equação temos:

32 μ 60 × 10 3 - 32 μ = cosh ⁡ 100 μ 60 × 10 3 - 32 μ - 1

Se plotarmos a equação:

f x = 32 x 60000 - 32 x - cosh ⁡ 100 x 60000 - 32 x + 1

Nós encontraremos f x = 0 em:

μ = 310.37   N / m

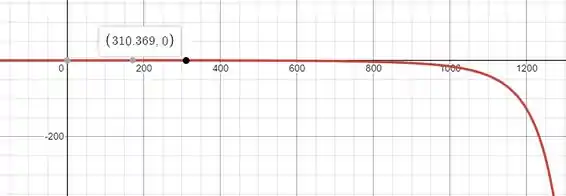
Essa densidade é a densidade máxima suportada para a corda poder ter a tração máxima.

Passo 3

Para encontrar a densidade do gelo precisamos converter essa densidade que acabamos de encontrar e tirar a densidade da corda da corda:

ρ g e l o = 310.37 9.81 - 18.2 = 13.44   k g / m

Resposta

ρ g e l o = 13.44   k g / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada cabo exerce uma força de 400N sobre o poste. Determine a intensidade da componente projetada de F 1 ao longo da linha de ação de F 2 .
Determine a intensidade da componente projetada da força F = 300N que atua ao longo da linha O A .
Determine o ângulo θ entre os cabos A B e A C .
Se F possui uma intensidade de 250N , determine a intensidade de suas componentes projetadas que atuam ao longo do eixo x e do cabo A C .
Determine os componentes x , y e z da força F que atua no tetraedro como mostrado. Os valores de a , b e c e F são conhecidos e M é o ponto médio da aresta A B .