Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 49

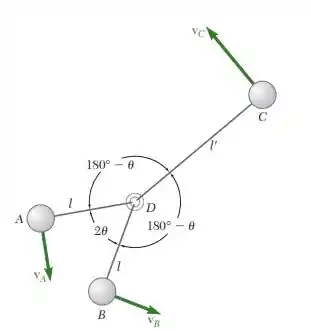
14.49. Três esferas idênticas A, B e C, que podem deslizar livremente sobre uma superfície horizontal sem atrito, estão ligadas por meios de cordas inelásticas e inextensíveis a um pequeno anel D localizados no centro de massa das três esferas (l 2l cos ). Inicialmente, as esferas giram em torno do anel D, que está em repouso, a velocidades proporcionais às suas distâncias de D. Indicamos v0 como a velocidade original de A e B e consideramos que 30°. Repentinamente a corda CD se parte, fazendo com que a esfera C deslize para longe. Considerando o movimento das esferas A e C, e do anel D após as outras duas cordas ficarem outra vez esticadas, determine (a) a velocidade do anel D, (b) a velocidade relativa com a qual a esfera A e a B rodam em torno de D, (c) a percentagem de energia do sistema original que é dissipada quando as cordas AD e BD ficam esticadas outra vez.

Passo 1

Para resolver esse problema podemos considerar dois instantes, o primeiro instante é logo quando a corda C D se parte. Nesse instante o momento linear é:

L 1 = 2 m v 0 cos ⁡ θ i ^

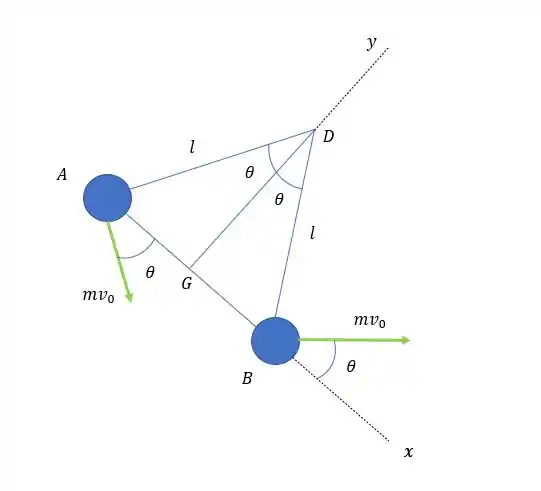
E o momento angular sobre o ponto G é

H G = 2   l sin ⁡ θ ⋅ m v 0 sin ⁡ θ     k ^

H G = 2 l m v 0 sin 2 ⁡ θ k ^

Passo 2

O segundo instante é logo depois que as cordas A D - e B D - ficam esticadas.

Agora o centro de massa está no ponto D. Então o momento linear fica:

L = 2 m v → = 2 m v 0 cos ⁡ θ i ^

No caso do problema temos

v D = v → = v 0 cos ⁡ θ

v D = v 0 cos ⁡ 30 ° = 0 , 866   v 0

Assim respondemos o item (a).

Passo 3

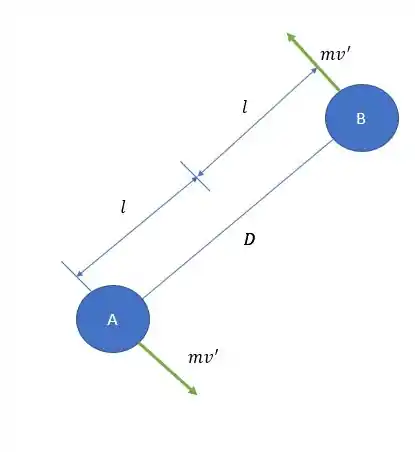
v ' é a velocidade relativa em que A e B rotacionam sobre D. Sendo assim, o momento angular sobre o ponto G fica

H G = 2 m v ' l

Mas nós já tínhamos calculado um valor para esse momento linear

H G = 2 l m v 0 sin 2 ⁡ θ k ^

Logo

2 m v ' l = 2 l m v 0 sin 2 ⁡ θ

Então

v ' = v 0 sin 2 ⁡ θ

Então

v ' = v 0 sin 2 ⁡ 30 ° = 0 , 25   v 0

Agora respondemos o item (b).

Passo 4

Vamos calcular a energia dissipada agora. Considerando as 3 esferas, temos

T 0 = 1 2 m v A 2 + v B 2 + v C 2 = m v 0 2 1 + 2 cos 2 ⁡ θ

E a energia cinética final fica

T f = 1 2 2 m v D 2 + 2 1 2 m v ' 2 + 1 2 m v C 2

Mas

v D = v C = v 0 cos ⁡ θ

T f = m v 0 2 cos 2 ⁡ θ + m v 0 sin 2 ⁡ θ 2 + 2 v 0 2 cos 2 ⁡ θ

T f = m v 0 2 3 cos 2 ⁡ θ + sin 2 ⁡ θ

Para calcular a dissipação de energia em porcentagem podemos fazer:

E P = 100 T 0 - T f T 0

Então

E P = 100 m v 0 2 1 + 2 cos 2 ⁡ θ - m v 0 2 3 cos 2 ⁡ θ + sin 2 ⁡ θ m v 0 2 1 + 2 cos 2 ⁡ θ

E P = 100 sin 2 ⁡ θ cos 2 ⁡ θ 1 + 2 cos 2 ⁡ θ

Então

E P = 100 sin 2 ⁡ 30 ° cos 2 ⁡ 30 ° 1 + 2 cos 2 ⁡ 30 ° = 7 , 5   %

Resposta

a : 0 , 866   v 0 b :   0 , 2 5   v 0 c : 7 , 5   %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de brinquedo é propelido por água que esguicha de um tanque interno a uma velocidade constante de 2 m/s em relação ao carro. O peso do carro vazio é de 200 g e este contém 1 kg de água. Despr
A profundidade da água que escoa do um canal de seção transversal retangular de largura b a uma velocidade v1 e a uma profundidade d 1 aumenta para uma profundidade d 2 em um ressalto hidráulico. Expr
Em uma roda de turbina Pelton, o jato de água é defletido por uma série de pás de modo que a taxa com a qual a água é defletida pelas pás é igual à taxa com a qual a água sai do bocal ( Δ m / Δ t = A
14.47. Duas pequenas esferas A e B, de massas 2,5 kg e 1 kg, respectivamente, estão unidas por uma barra rígida de massa desprezível. As duas esferas estão em repouso sobre uma superfície horizontal s