Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 89

Um carro de brinquedo é propelido por água que esguicha de um tanque interno a uma velocidade constante de 2 m/s em relação ao carro. O peso do carro vazio é de 200 g e este contém 1 kg de água. Desprezando outras forças tangenciais, determine sua velocidade máxima.

Passo 1

Vamos lá resolver mais essa. Vamos considerar que o movimento ocorre em um intervalo de tempo Δ t . No movimento, temos a seguinte configuração de forças:

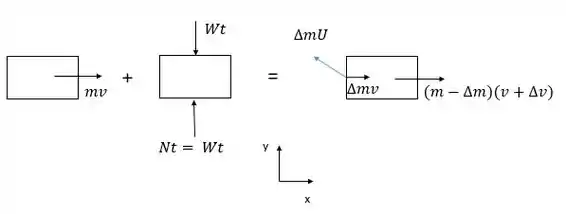
Aqui, m representa a massa total do sistema (carro + tanque de água), que tem massa inicial m 0 e massa final ( m - Δ m ) , e v é a velocidade do carro. Utilizando o princípio de impulso, temos:

m v + 0 = Δ m v - U cos ⁡ θ + ( m - Δ m ) ( v + Δ v )  

m - Δ m v = m - Δ m v + m - Δ m Δ v - Δ m ( U cos ⁡ θ )

Δ v = U cos ⁡ θ Δ m m - Δ m

Essa expressão representa a variação de velocidade nesse intervalo de tempo.

Passo 2

Agora, vamos achar uma função que relacione a perda de massa com a velocidade do carro. Para isso, vamos substituir Δ v por dv e Δ m por –dm, já que a massa total do conjunto vai diminuindo:

d v =   - U cos ⁡ θ d m m

∫ v 0 v d v =   - ∫ m 0 m U cos ⁡ θ d m m → v = v 0 - U cos ⁡ θ ln ⁡ m m 0

Como v 0 = 0,

v = U cos ⁡ 20 ° ln ⁡ m 0 m

Passo 3

A velocidade máxima será quando a massa final do conjunto for igual ao peso vazio do carro. Assim:

v m á x = 2 cos ⁡ 20 ° ln ⁡ 1 + 0,2 0,2

v m á x = 3,37   m / s

Resposta

v m á x = 3,37 m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.107. Três vagões de carga idênticos têm as velocidades indicadas na figura. Considerando que o vagão B é primeiramente atingido pelo vagão A, determine a velocidade de cada vagão após todas as coli
14.110. Um bloco de 9 kg parte do repouso e desce deslizando sobre a superfície inclinada de uma cunha A de 15 kg que está apoiada sobre uma superfície horizontal. Desprezando o atrito, determine (a)
14.108. Um helicóptero A de 4.500 kg estava viajando para o leste em voo nivelado a uma velocidade de 120 km/h e uma altitude de 750 m quando foi atingido por um helicóptero B de 6.000 kg. Como result
Para uma certa velocidade do vento, a turbina eólica mostrada na figura produz 28 kW de eletricidade e tem uma eficiência de 0,35 no sistema de conversão de energia. Considerando ρ = 1,21 kg/m³ para o
A hélice de um pequeno avião tem uma corrente de ar produzida de 2 m de diâmetro, gerando um empuxo de 4.000 N quando o avião está parado no solo. Considerando γ = 1,21 kg/m³ para o ar, determine (a)