Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 145

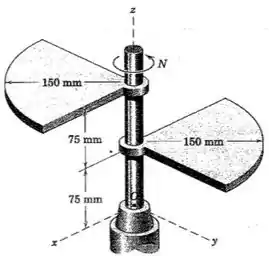
145. Calcule o momento fletor M no eixo O para o conjunto em rotação do Prob 7 / 144 , quando parte do repouso com uma aceleração angular inicial de 200   r a d / s 2 .

Passo 1

Bom, primeiro vamos definir como m sendo a massa de cada placa.

A massa por unidade de área, lembrando que uma placa é um quarto de círculo:

δ = m π R 2 4

δ = 4 m π R 2

Passo 2

Para tamanhos infinitesimais de ângulo, massa e tamanho:

d m = 4 m π R 2 r d r d θ

Agora, calcularemos o momento de inércia I x z :

  I x z = ∫ x z d m

I x z = 4 m π R 2 ∫ 0 π 2 ∫ 0 R r ⋅ cos ⁡ θ ( x   m )   r   d r   d θ

I x z = 4 m π R 2 ∫ 0 π 2 ( R 3 - 0 3 ) ( x   m ⋅ c o s ⁡ ( θ ) )   3   d θ

I x z = 4 m π R 2 ∫ 0 π 2 R 3 ( x   m ⋅ c o s ⁡ ( θ ) )   3 d θ

I x z = 4 m π R 2 ( sen ⁡ π / 2 - s e n ⁡ ( 0 ) ) ( R 3 ⋅ x   m )   3

I x z = 4 m π R 2 ( 1 - 0 ) ( R 3 ⋅ x   m )   3

∴ I x z = 4 x m R 3 π   k g ⋅ m 2

E agora, o momento de inércia I y z :

  I y z = ∫ y z d m

I y z = 4 m π R 2 ∫ 0 π 2 ∫ 0 R - r ⋅ sen ⁡ θ ( x   m )   r   d r   d θ

I y z = - 4 m π R 2 ∫ 0 π 2 ( R 3 - 0 3 ) ( 0,150 x   m ⋅ s e n ⁡ ( θ ) )   3   d θ

I y z = - 4 m π R 2 ∫ 0 π 2 R 3 ( x   m ⋅ s e n ⁡ ( θ ) )   3 d θ

I y z = - 4 m π R 2 - ( cos ⁡ π / 2 - c o s ⁡ ( 0 ) ) ( R 3 ⋅ x   m )   3

I y z = - 4 m π R 2 - ( - 0 - 1 ) ( R 3 ⋅ x   m )   3

∴ I y z = - 4 x m R 3 π   k g ⋅ m 2

Aqui, x é a distância do ponto O até a placa em questão.

Passo 3

Para a placa superior:

I x z = - I y z = 4 ( 0,150   m ) ( 2   k g ) ( 0,150   m ) 3 π   k g ⋅ m 2

I x z = - I y z = 0,01910   k g ⋅ m 2

Já para a placa inferior, como a placa está na metade do caminho, em vez de 0,150   m , o valor de x será 0,075   m , portanto, é só dividir o momento de inércia achado para a placa superior por dois:

I x z = - I y z = 0,01910 2 = 0,00955   k g ⋅ m 2

Passo 4

Como não há rotação nos eixos x e y , então:

ω x = ω y = ω z = 0

Mas, há aceleração angular, que é dada por:

ω ˙ z = 200   r a d / s 2

Passo 5

Como nós já temos as equações prontas:

∑ M x = - I x z ω ˙ z

∑ M y = - I y z ω ˙ z

∑ M z = 0

Para M x , substituindo os valores:

M x = - ( 0,01910   k g ⋅ m 2 - 0,00955   k g ⋅ m 2 ) ( 200   r a d / s 2 )

M x = - ( 0,00955   k g ⋅ m 2 ) ( 200   r a d / s 2 )

∴ M x = - 1,910   N ⋅ m

Para M y , substituindo os valores:

M y = - ( - 0,01910   k g ⋅ m 2 + 0,00955   k g ⋅ m 2 ) ( 200   r a d / s 2 )

M y = - ( - 0,00955   k g ⋅ m 2 ) ( 200   r a d / s 2 )

∴ M y = 1,91   N ⋅ m

Passo 6

O momento total M será dado por:

M = M x 2 + M y 2

M = 1,91     N ⋅ m 2 + 1,91     N ⋅ m 2

M = 3,6481   N ⋅ m 2 + 3,6481 N ⋅ m 2

M = 7,2962   ( N ⋅ m ) 2

∴ M = 2,70   N ⋅ m

Resposta

O momento fletor M será:

M = 2,70   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

118. Os dois discos circulares idênticos, cada um de massa m e raio r , estão girando com uma unidade rígida em torno de seu eixo comum. Determine o valor de b para o qual não ocorrerá movimento de pr
120. A figura mostra uma bola de futebol americano em três configurações comuns durante o vôo. O caso (a) é um passe em espiral arremessado perfeitamente com uma velocidade de giro de 120r p m . O cas
125. Os dois cones circulares retos homogêneos maciços, cada um de massa m , são fixados um ao outro em seus vértices para formar uma unidade rígida e estão girando em torno de seu eixo de simetria ra
124. O satélite de observação da Terra está em uma órbita circular de período τ . A velocidade angular do satélite em torno de seu eixo y ou eixo de arfagem é ω = 2 π / τ , e as velocidades angulares
128. Se o navio do Exemplo 7 / 8 está em curso reto, mas a sua proa está abaixando enquanto cai no vale de uma onda, determine o sentido do momento giroscópico exercido pelo rotor da turbina sobre a e