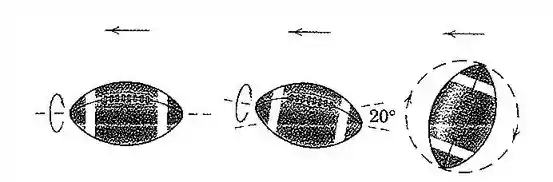
120. A figura mostra uma bola de futebol americano em três configurações comuns durante o vôo. O caso (a) é um passe em espiral arremessado perfeitamente com uma velocidade de giro de . O caso (b) é um passe em espiral com oscilação novamente com uma velocidade de giro de em torno de seu próprio eixo, mas com o eixo oscilando através de um ângulo total de . O caso (c) é um chute dado na bola em repouso e que segue girando em torno de seu eixo transversal com uma velocidade de rotação de . Para cada caso, especifique os valores de e conforme definido nesta seção. O momento de inércia em relação ao eixo maior da bola é vez aquele em relação ao eixo transversal de simetria.

(a) Temos então para o primeiro, em que o passe em espiral arremessado perfeitamente com uma velocidade de giro de , a taxa precessional vai ser igual a zero, de modo que os ângulos e também vão valer zero.

Só nos resta calcular o valor do giro , dado por:

(b) Para este caso, já sabemos o valor do giro que é igual a , e do ângulo de . Falta calcular o valor da taxa precessional , dada por:

E o ângulo , nós calculamos através da seguinte relação:

(c) E para o último caso, já temos o valor de e de , que valem . Além disso, como o chute foi dado na bola em repouso e ela segue girando em torno de seu eixo transversal, a velocidade de giro vai valer zero (). Este é um caso especial e quando ele ocorre a taxa precessional vai ser igualzinha ao valor da velocidade de rotação: