Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 118

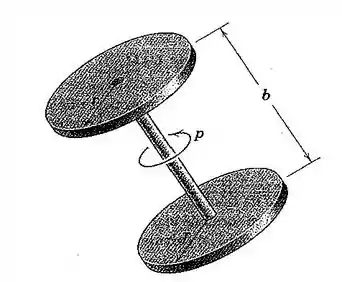
118. Os dois discos circulares idênticos, cada um de massa m e raio r , estão girando com uma unidade rígida em torno de seu eixo comum. Determine o valor de b para o qual não ocorrerá movimento de precessão se a unidade está livre para se deslocar no espaço.

Passo 1

Como estamos trabalhando com precessão e consequentemente, com momento de inércia, vamos fazer um esboço do nosso sistema de discos em relação a um sistema de coordenadas tridimensional:

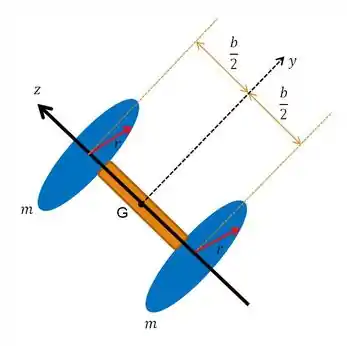
Passo 2

A taxa precessional de oscilação ψ ˙ é dada por:

ψ ˙ = I p I 0 - I ⋅ cos ⁡ θ

Onde I   é o momento de inércia em relação ao eixo maior da bola e I 0 o momento em relação ao eixo transversal de simetria:

ψ ˙ = I p I 0 - I ⋅ cos ⁡ θ

Só que olhando aquela obra de arte que fizemos no P a s s o   1 , perecebe-se que os momento de inércia I e I 0 , são os momentos em relação aos eixos z e y , respectivamente, os quais são dados abaixo. Vale ressaltar que para o cálculo do momento I y y , é preciso recorrer ao teorema dos eixos paralelos, considerando uma distância de b / 2 entre o eixo y e os discos.

I = I z z = 2 ⋅ 1 2 m r 2 I 0 = I y y = 2 ⋅ 1 4 m r 2 + m b 2 2

Passo 3

E para que não ocorra precessão, tem que ser satisfeita a seguinte condição:

I 0 = I

2 ⋅ 1 4 m r 2 + m b 2 2 = 2 ⋅ 1 2 m r 2

1 2 m r 2 + 1 2 m b 2 = m r 2

1 2 m b 2 = 1 2 r 2

b 2 = r 2

b = r

Resposta

b = r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
O guindaste possui uma lança de comprimento OP = 24 m e está girando em torno do eixo vertical na taxa constante de 2 rpm no sentido indicado. Simultaneamente, a lança está sendo abaixada na taxa cons
O disco circular de 120 mm de raio gira em torno do eixo z na taxa constante de w = 20 rad/s, e o conjunto inteiro gira em torno do eixo fixo x na taxa constante wx = 10 rad/s. Calcule os módulos da v
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c