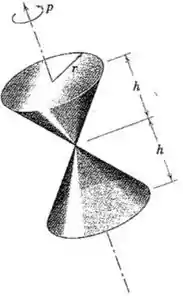
125. Os dois cones circulares retos homogêneos maciços, cada um de massa , são fixados um ao outro em seus vértices para formar uma unidade rígida e estão girando em torno de seu eixo de simetria radial à taxa de .

(a) Determine a razão para a qual o eixo de rotação não realiza precessão.

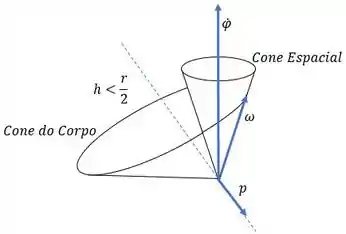
(b) Esboce os cones espacial e do corpo para o caso onde é menor do que a razão crítica.

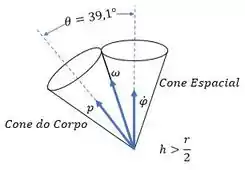
(c) Esboce os cones espacial e do corpo quando e a velocidade de precessão é .

(a) Para o caso de não termos precessão, então .

Da tabela que informa como que fica os momentos de inércia do objeto, nós temos:

Aqu, tivemos que multiplicar ambos momentos de inércia por , pois a tabela fornece dados para um “cone”. Para calcular nós ultilizamos o teorema dos eixos paralelos.

Como , então:

(b) Para menor que a razão crítica, temos , portanto:

O que resulta em uma precessão retrógrada

(c) Para , nós temos:

Agora, da fórmula da velocidade de precessão:

Temos:

Como temos o valor do giro em torno do seu eixo em , precisamos encontrá-la em :

Agora, pela fórmula:

Dividiremos o valor de por :

Calculando o

O que resulta em uma precessão direta