Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 146

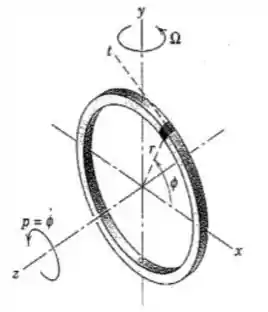
146. Desenvolva a Eq. 7 / 24 , relacionando as forças às acelerações para um elemento diferencial do anel fino de massa m . O anel possui uma velocidade angular constante p em torno do eixo z e recebe uma velocidade angular constante adicional de Ω em torno do eixo y por meio da aplicação de um momento externo M (não mostrado). (Sugestão: A aceleração do elemento na direção z é devido (a) à variação no módulo da componente de sua velocidade nessa direção em consequência de Ω e (b) à variação na direção da componente x de sua velocidade.

Passo 1

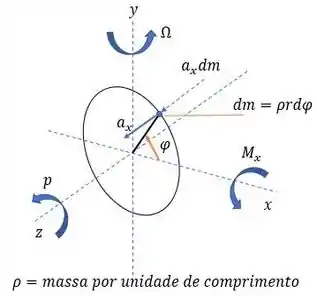
Bom, primeiro vamos esquematizar tudo que está acontecendo nessa situação:

Passo 2

Assumiremos que a x d m é a única força em d m que exerce um momento nos eixos x e y .

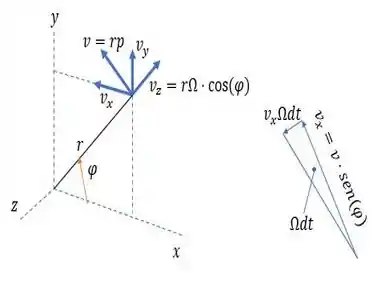
A aceleração na direção z devido à mudança de direção de v x será:

v x Ω = r Ω p ⋅ s e n ( φ )

A aceleração na direção z devido à mudança de magnetude de v z será:

- d d t r Ω ⋅ cos ⁡ φ = r Ω φ ˙ ⋅ s e n φ = r Ω p ⋅ s e n ( φ )

Portanto, a aceleração na direção z será:

a z = 2 r p Ω ⋅ s e n ( φ )

Passo 3

O momento M x que atua no eixo x será:

M x = ∫ r ⋅ s e n ( φ ) ( a x d m )

M x = ∫ r ⋅ s e n ( φ ) ( 2 r p Ω ⋅ s e n ( φ ) ) ( ρ r d φ )

M x = 2 ρ r 3 p Ω ∫ 0 2 π s e n φ 2 d φ

M x = 2 ρ r 3 p Ω 1 2 ( 2 π - s e n 2 π ⋅ cos ⁡ 2 π ) - 1 2 ( 0 - s e n 0 ⋅ cos ⁡ 0 )

M x = 2 ρ r 3 p Ω π

∴ M x = m r 2 p Ω = I Ω p   ( N / m )

Já o momento M y que atua no eixo y será:

M y = - ∫ r ⋅ c o s ( φ ) ( a x d m )

M y = ∫ r ⋅ c o s ( φ ) ( 2 r p Ω ⋅ s e n ( φ ) ) ( ρ r d φ )

M y = 2 ρ r 3 p Ω ∫ 0 2 π s e n φ ⋅ c o s ⁡ ( φ ) d φ

M y = 2 ρ r 3 p Ω - 1 2 ⋅ c o s ⁡ ( 2 π ) 2 - - 1 2 ⋅ c o s ⁡ ( 0 ) 2

M y = 2 ρ r 3 p Ω - 1 2 ⋅ 1 2 - - 1 2 ⋅ 1 2

M y = 2 ρ r 3 p Ω - 1 2 + 1 2

M y = 2 ρ r 3 p Ω ⋅ ( 0 )

M y = 0   N / m

Passo 4

O momento total M será dado por:

M = M x 2 + M y 2

M = I Ω p N ⋅ m 2 + 0     N ⋅ m 2

M = I Ω p 2   N ⋅ m 2 + 0 2   N ⋅ m 2

M = I Ω p 2   ( N ⋅ m ) 2

∴ M = I Ω p   N ⋅ m

Resposta

O momento fletor M será:

M = I Ω p   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

142. O desbalanceamento dinâmico de um determinado virabrequim é aproximado pela modelo físico apresentado, onde o eixo sustenta três esferas pequenas de 0,6k g fixadas por hastes de massa desprezível
144. Cada uma das placas com o formato de um quadrante de círculo possui uma massa de 2k g e está presa ao eixo vertical montado no mancal fixo em O . Calcule o módulo M do momento fletor no eico em O
O carrinho e sua carga têm uma massa total de 100k g . Determine a aceleração do carrinho e as reações normais sobre o par de rodas em A e B . Despreze a massa das rodas.
No instante mostrado, ambas as barras de massa desprezível balançam com uma velocidade angular no sentido anti-horário ω = 5r a d / s , enquanto a barra de 50k g está sujeita à força horizontal de 100
Se o armário de 80k g é liberado para rolar para baixo sobre o plano inclinado, determine a aceleração do armário e as reações normais sobre o par de roletes em A e B que têm massa desprezível.