Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 145

145- A correia plana tem largura b = 50   m m e está no limiar de deslizar conforme ela puxa a polia com raio r = 75   m m através de um ângulo de contato de 180. Se a força trativa no lado frouxo da correia é de T 1 = 1000   N   , faça um gráfico da pressão normal p entre a correia e a polia, em função de θ entre θ = 0 e θ = π . Especifique as pressões máxima e mínima p 1 e p 2 , a força trativa T 2 . E o torque reativo M sobre o eixo da polia. O coeficiente de atrito entre a correia e a polia vale 0.30 . (Os mancais da polia não estão mostrados)

Passo 1

Como o lado T 1 é o lado frouxo da correia logo a força T 2 será:

T 2 = T 1   e μ β

Onde T 1 vale 1000   N , β = π   r a d e μ = 0.3 logo a força T 2 será:

T 2 = 1000 × e 0.3 × π = 2566.33   N

Com isso o momento presente na polia será de:

M = 2566.33 - 1000 × 75 × 10 - 3 = 117.47   N m

Passo 2

Para calcular a pressão nós precisamos da expressão que da origem a fórmula do cálculo de tração das polias que é:

d N = T d θ

Onde T é a o lado mais tensionado e valerá:

T = T 1 e μ θ

E d N é a normal que sai da polia e que pode ser calculado por:

N = P × A

d N = P   d A

Onde a área é a área de contato da polia com a correia, que é o cilindro de altura b e raio r . Logo:

d A = r b   d θ

Pois assim que a área superficial de um cilindro é dada por 2 π r h para uma seção de circulo que vai de 0 até 2 π ela valerá θ r b para um setor circular que vai de 0 a θ . Logo:

P r b   d θ = T 1 e μ θ

P = T 1 r b   e μ θ

Para uma força de tração igual a 1000   N temos uma pressão igual a:

P = 1000 75 × 10 - 3 × 50 × 10 - 3 × e 0.3 × θ = 266.67   e 0.3 θ [ k P a ]

Passo 3

Plotando o gráfico com θ variando de 0   até 180 graus temos:

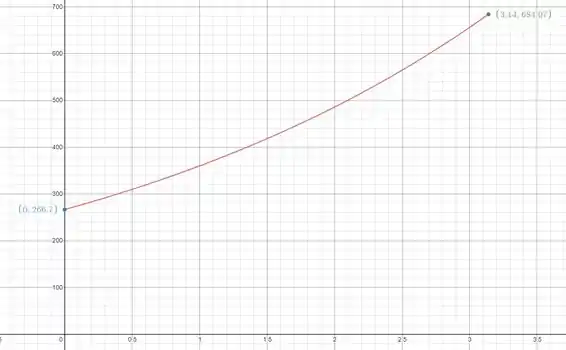
Cuja menor pressão vale 266.7   k P a e a maior 684.07   k P a

Resposta

T 2 = 2566.33   N

M = 117.47   N m

P 1 = 266.7   k P a

P 2 = 684.07   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco com diâmetro externo de 120 mm se encaixa livremente em um eixo fixo com diâmetro de 30 mm. Se o coeficiente de atrito estático entre o disco e o eixo é μ s = 0,15 e o disco possui massa de 5
A embreagem de disco é composta de uma placa plana A que desliza sobre o eixo giratório S , o qual é fixado na engrenagem motriz B . Se a engrenagem C , que está entrosada com B , está sujeita a um to
O apoio axial está sujeito a uma distribuição de pressão em sua superfície de contato que varia conforme mostra a figura. Se o coeficiente de atrito estático é μ , determine o torque M necessário para
A luva encaixa-se livremente em torno de um eixo fixo com raio de 50 mm. Se o coeficiente de atrito cinético entre o eixo e a luva é μ k = 0,3 , determine a força P no segmento horizontal da correia d
O  mancal  de  escora  suporta  uniformemente  uma força axial  P=   5   k N . Se o coeficiente de atrito  estático é  u s=   0,3 , determine o torque M necessário  para superar o atrito.