Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 133
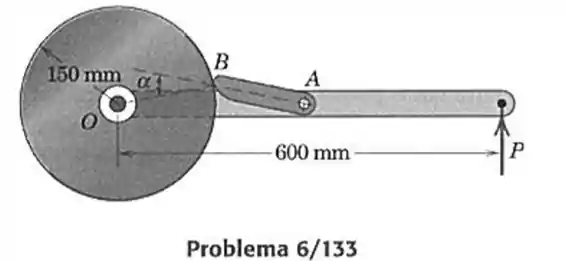
133- A figura mostra uma chave a fricção para girar a roda no sentido anti-horário sob a ação de uma força aplicada ao cabo. O conector flutuante se prende a roda de forma que . Se uma força é necessária para girar a roda em torno do seu mancal em , determine o coeficiente de atrito estático mínimo entre o conector e a roda que garantirá que não haja deslizamento em e o módulo da força sobre o pino em .
Passo 1
O momento que aplica no centro da roda é de:
Passo 2
Agora vamos desenhar o sistema de forças do mecanismo:
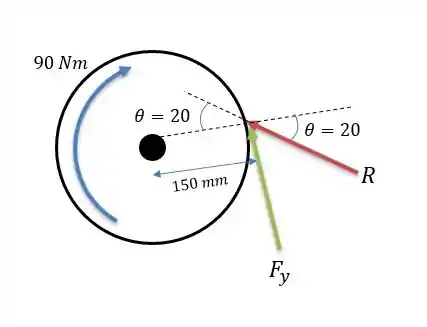
Onde expressamos a reação do momento aplicado por e o ângulo que faz com o disco. Podemos calcular projetando seu vetor perpendicularmente ao raio tal que:
Onde a força faz um momento em relação a .
Logo será:
Passo 3
O menor atrito possível é o atrito causado pelo próprio ângulo de .