Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 58
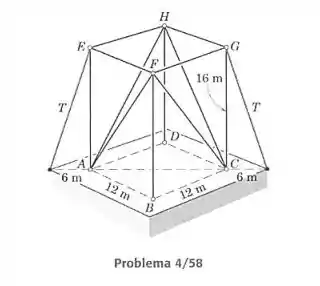
A treliça espacial com 16 m de altura é erguida sobre uma base horizontal quadrada com 12 m de lado. Cabos de amarração são presos à estrutura em e como mostrado e são esticados até que a tração em cada cabo valha 9 kN. Calcule a força em cada elemento diagonal.
Passo 1
Vamos calcular as forças pelo método dos nós, aplicando as três equações de equilíbrio (para , e ) para os pontos de interseção dos elementos da treliça. A primeira coisa a se notar aqui é a simetria que existe na estrutura, em relação ao plano que contém e em relação ao plano que contém . Essa simetria nos permite identificar as seguintes igualdades entre as forças:
- Todas as forças diagonais são iguais:
- Todas as forças dos elementos horizontais do topo da treliça são iguais:
- As forças dos elementos verticais opostos são iguais:
Essas igualdades facilitarão nosso cálculo.
Passo 2
Agora temos qu escolher um nó para fazer as equações e encontrar as forças. Devemos pegar um ponto de cima, pois em baixo temos forças desconhecidas e teremos mais trabalho. Nos nós e , temos as forças desconhecidas dos elementos horizontais que chamaremos de (), as forças dos elementos verticais e as forças diagonais que queremos encontrar. Já nos pontos e temos menos incógnitas. Vamos olhar o ponto :
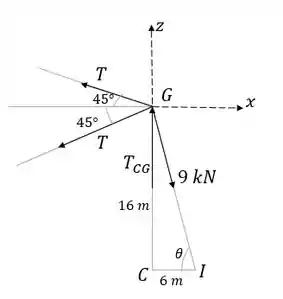
Posicionamos os eixos coordenados de maneira conveniente pra calcular as equações de equilíbrio. Como só estamos interessados em achar o valor de (pois ele está presente nos nós e que é onde obteremos ), fazemos a soma das forças no eixo :
Achamos facilmente da seguinte maneira:
Então substituindo os cossenos achamos :
Passo 3
Vamos olhar agora para o ponto , posicionando de maneira diferente os eixos , e :
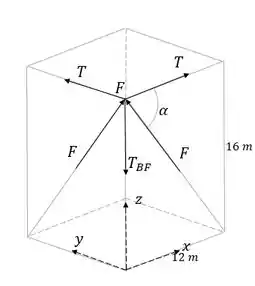
Para evitar a incógnita , fazemos a soma das forças no eixo :
Achamos assim:
Então:
Como podemos ver no desenho e o sinal deu positivo, a força do elemento é de contração. Pela simetria, então encontramos todos os elementos diagonais: