Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 51
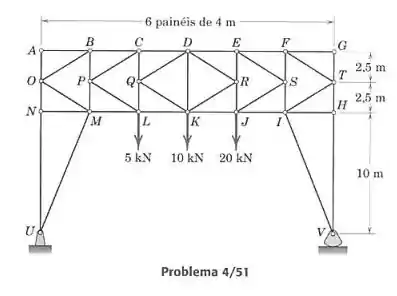
Determine a força no elemento da treliça para placas de sinalização carregada.
Passo 1
Devemos calcular para essa treliça as forças pelo método das seções, fazendo um corte na treliça e pegando parte dela como se fosse um corpo rígido, então aplicando as equações de equilíbrio para esse corpo. Não conseguimos fazer um corte passando por e poucos elementos (os cortes passando por ele tem no mínimo 5 forças desconhecidas envolvidas), então teremos que fazer cortes mais de uma vez, até termos um número de incógnitas pequeno o suficiente para encontrar . O primeiro corte que será feito passará por , , e , pegando a parte esquerda:
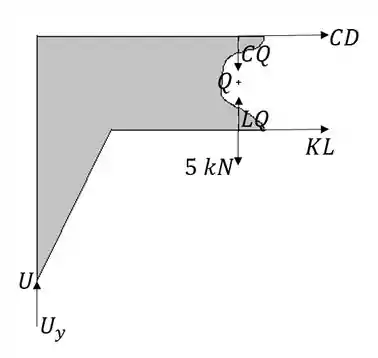
Só estamos interessados nas forças e , que vão pra direita para próximo de . Para achar , podemos calcular o momento em torno de . Mas pra isso precisamos da força vertical , então focaremos primeiro em encontrar as forças externas.
Passo 2
Observando o formato do apoio em , percebemos fazilmente que os apoios em e não fazem força na direção horizontal. Obtemos diretamente fazendo o momento em torno de da treliça como um todo:
Agora fazenso o equilíbrio das forças verticais achamos :
Passo 3
Agora podemos olhar pra nossa parte da treliça e calcular através do momento em relação a :
O valor negativo indica que a força é de compressão (apontando o nó) e não de tração como desenhamos. Agora pelo simples equilíbrio das forças horizontais sabemos que:
Fazendo uma analogia ao outro lado da treliça, se fizéssemos um corte exatamente igual, passando por , , e , teríamos o seguinte:
Então temos:
E também:
Passo 4
Agora se olharmos para o ponto temos nele 3 forças desconhecidas e 2 desconhecidas. Pra fazer as equações de equilíbrio e resolver precisamos ter apenas 2 incógnitas, então ainda precisamos antes achar mais forças. Vamos agora fazer um corte passando por , , e :
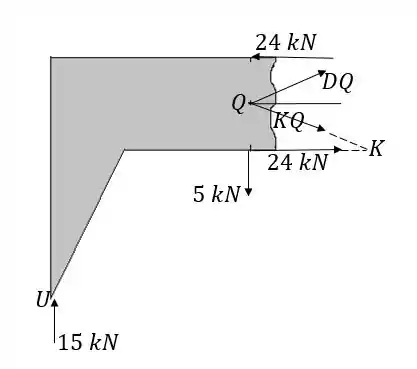
Fazendo o momento em relação a conseguimos achar diretamente, mas precisamos do seno e do cosseno do ângulo . Encontramos eles rapidamente da seguinte forma:
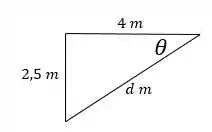
Agora podemos calcular o momento em torno de :
O sinal negativo indica que a força é de compressão e não de tração. Agora só temos duas incógnitas no ponto D! Com as 2 equações de equilíbrio, somos capazes de encontrar .
Passo 5
Vamos dar uma olhada nas forças no ponto . Perceba que agora já conseguimos representar todas as forças no sentido correto ( é de tração):
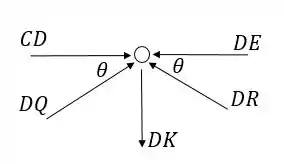
Vamos então às equações de equilíbrio:
Agora substituindo os valores já encontrados das forças e do cosseno:
Agora para o eixo :