Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 142

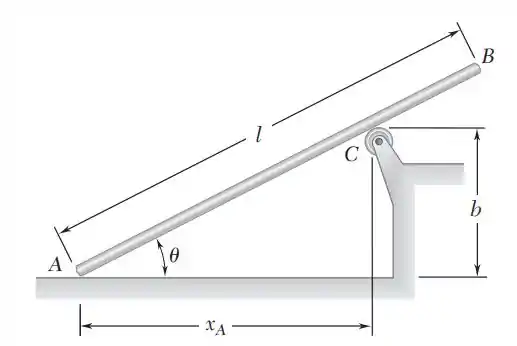
15.141. A barra AB desloca-se sobre um rolete em C enquanto a extremidade A se move para a direita com uma velocidade constante v A . Usando o método da Seção 15.9, deduza expressões para a velocidade angular e para a aceleração angular da barra.

Passo 1

Vamos começar mais uma! A gente pode usar esse triângulo aqui:

Em que

x A + x B = x

b + b ' = y

De acordo com o método da seção 15.9 temos

x = l cos ⁡ θ y = l sin ⁡ θ

Podemos definir os valores de sin ⁡ θ e cos ⁡ θ usando o triangulo interno. Olha só:

sin ⁡ θ = c a t e t o   o p o s t o h i p o t e n u s a

Usando o triangulo interno

sin ⁡ θ = b x A 2 + b 2

E

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a

Então

cos ⁡ θ = x A x A 2 + b 2

Então a gente fica com

x = l cos ⁡ θ

x = l x A x A 2 + b 2

E

y = l sin ⁡ θ

y = l b x A 2 + b 2

Passo 2

Beleza, agora temos os valores de x e y . Podemos substituir esses valores nas equações

x A + x B = x

x B = x - x A

Logo

x B = l x A x A 2 + b 2 - x A

E analogamente

b + b ' = y

b = y - b '

Logo

b ' = l b x A 2 + b 2 - b

Agora a gente deriva.

x ˙ B = d d t l x A x A 2 + b 2 - x A

Isso fica

x ˙ B = l d d t x A x A 2 + b 2 - d d t x A

Então

x ˙ B = l d d t x A x A 2 + b 2 - x ˙ A

Vamos usar a regra do produto

x ˙ B = l d d t x A ⋅ 1 x A 2 + b 2 + d d t 1 x A 2 + b 2 ⋅ x A - x ˙ A

Isso fica

x ˙ B = l x ˙ A x A 2 + b 2 - 2 x A x ˙ A x A 2 + b 2 3 2 - x ˙ A

Isso fica

x ˙ B = l b 2 x ˙ A x A 2 + b 2 3 2 - x ˙ A

Passo 3

Vamos fazer o mesmo para b '

b ' ˙ = d d t l b x A 2 + b 2 - b

Tirando a constantes

b ' ˙ = l d d t b x A 2 + b 2 - b

Agora usamos a regra do produto

b ' ˙ = l d d t b ⋅ 1 x A 2 + b 2 + d d t 1 x A 2 + b 2 ⋅ b - b ˙

Isso fica

b ' ˙ = l b ˙ x A 2 + b 2 - 2 x A x ˙ A x A 2 + b 2 3 2 - b ˙

Então

b ' = - l b x A x A ˙ x A 2 + b 2 3 2

Mas sabemos que

x A ˙ = - v A x B ˙ = v B x b ' ˙ = v B y

Então

v B x = v A - l b 2 x ˙ A x A 2 + b 2 3 2

E

v B y = l b x A v A x A 2 + b 2 3 2

Resposta

v B x = v A - l b 2 x ˙ A x A 2 + b 2 3 2

v B y = l b x A v A x A 2 + b 2 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s no sentido horário, determine a aceleração angular (a) da barra BD, (b) da barra DE.
Sabendo que, no instante mostrado na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular constante de ω 0 no sentido horário, determine (a) a aceleração angular do braço DE, (b
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s no sentido horário, determine a aceleração angular (a) da barra BD, (b) da barra DE.
Sabendo que, no instante mostrado na figura, a barra AB tem uma velocidade angular constante de 6 rad/s no sentido horário, determine (a) a aceleração angular do membro BDE, (b) a aceleração do ponto
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s e uma aceleração angular de 2 rad/s², ambas no sentido horário, determine a aceleração angu