Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 238

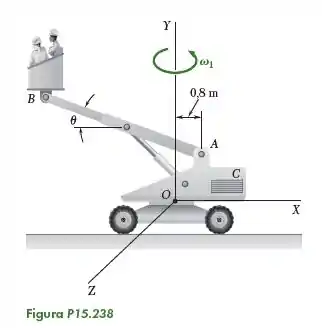
O braço A B de 5   m de comprimento é usado para fornecer uma plataforma elevada para trabalhadores da construção civil. Na posição mostrada na figura, o braço A B está sendo erguido a uma taxa constante d θ / d t = 0,25   r a d / s ; simultaneamente, a unidade está sendo girada em torno do eixo Y a uma taxa constante ω 1 = 0,15   r a d / s . Sabendo que θ = 20 ° , determine a velocidade e a aceleração do ponto B .

Passo 1

Oi pessoal... O exercício nos pede para determinar a velocidade e a aceleração do ponto B quando d θ / d t = 0,25   r a d / s e ω 1 = 0,15   r a d / s .

A velocidade escalar do ponto B será:

v B = v B ' + v B / F

Sabendo que:

v B ' = Ω × r B / O

v B / F = ω 2 × r B / A

E:

Ω = ω 1 j

ω 2 = - ω 2 k

Vamos aos cálculos.

Passo 2

Temos os seguintes vetores posições de B com relação a A e O , respectivamente:

r B / A = - 5 cos ⁡ 20 ° i + 5 sen ⁡ 20 ° j

r B / A = - 4,6985 i + 1,7101 j

E:

r B / O = r B / A - r A / O

Como r A / O = 0 , 8 i . Temos que:

r B / O = - 4,6985 i + 1,7101 j - 0 , 8 i

r B / O = - 3,898 i + 1,7101 j

Passo 3

Portanto:

v B ' = Ω × r B / O

v B ' = 0,15 j × - 3,898 i + 1,7101 j

v B ' = 0,58477 k   m / s

E:

v B / F = ω 2 × r B / A

v B / F = - 0,25 k × - 4,6985 i + 1,7101 j

v B / F = - 4 , 42753 i + 1 , 17462 j   m / s

Logo, a velocidade escalar do ponto B será:

v B = v B ' + v B / F

v B = 0,58477 k   + - 4,42753 i + 1,17462 j

Organizando e arredondando, temos que:

v B = - 4,42 8 i + 1,17 5 j + 0,58 5 k   m / s

Passo 4

Para a aceleração do ponto B , temos que:

a B = a B ' + a B / F + 2 Ω × v B / F

Temos que:

a B ' = Ω × v D / A

a B / F = ω 2 × v D / B

Portanto:

a B ' = 0,15 j × 0,58477 k

a B ' = ( 0 , 087715   m / s 2 ) i

Temos também que:

a B / F = - 0,25 k × - 4,42753 i + 1,17462 j

a B / F = 0,29365 i + 0,10688 j   m / s 2

Portanto:

a B = a B ' + a B / F + 2 Ω × v B / F

a B = ( 0,087715 ) i + 0,29365 i + 0,10688 j + 2 0,15 j × - 4,42753 i + 1,17462 j

a B = 0,381 i + 0,1069 j - 0,1283 k   m / s 2

Resposta

v B = - 4,428 i + 1,175 j + 0,585 k   m / s

a B = 0,381 i + 0,1069 j - 0,1283 k   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 15.182 considerando que o bloco A se desloca para a esquerda com velocidade constante de 2m / s .
A barra AB passa por meio de um colar que está soldado na ligação DE. Sabendo que no instante mostrado o bloco A se desloca para a direita em uma velocidade constante de 2m / s , determine (a) a veloc
15.222. A placa circular mostrada na figura gira em torno de seu diâmetro vertical a uma taxa constante 1 10 rad /s. Sabendo que na posição mostrada o disco se encontra no plano XY e o ponto D da alça
15.220. A barra AB está soldada em uma placa de 300 mm de raio que gira com uma taxa constante 1 6 rad /s. Sabendo que o colar D se desloca na direção da extremidade B da barra a uma velocidade consta
15.221. A barra dobrada mostrada na figura gira à taxa constante 1 3 rad /s. Sabendo que o colar C se desloca na direção do ponto D com uma velocidade relativa constante u 1 m/s, determine, para a pos