Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 135

Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s e uma aceleração angular de 2 rad/s², ambas no sentido horário, determine a aceleração angular (a) da barra BD, (b) da barra DE usando a aproximação do vetor como foi feito no Problema Resolvido 15.8.

Passo 1

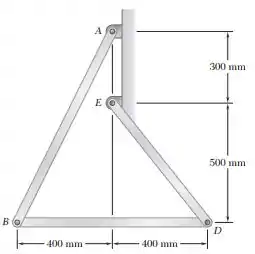
Vamos resolver mais essa. Como este problema envolve vários movimentos relativos entre os pontos de cada barra, vamos descrever primeiro os vetores posição relativa de cada barra:

r → B / A = - 400 i → - 800 j →

r → D / B = 800 i →

r → D / E = 400 i → - 500 j →

Agora vamos fazer uma análise de velocidade em cada barra. Para a barra AB:

ω → A B = - 4 k →

v → B = ω → A B × r → B / A = - 4 k → × ( - 400 i → - 800 j → )

v → B = - 3200 i → + 1600 j →

Para a barra BD:

ω → B D = ω B D k →

v → D = v → B + ω → B D × r → D / B =   - 3200 i → + 1600 j → + ω B D k → × 800 i →

v → D =   - 3200 i → + 1600 + 800 ω B D j →

Para a barra DE:

ω → D E = ω D E k →

v D = ω → D E × r → D / E = ω D E k → × ( 400 i → - 500 j → )

v → D = 500 ω D E i → + 400 ω D E j →

Igualando as componentes para as duas expressões referentes a v → D :

- 3200 = 500 ω D E → ω D E =   - 6,4   r a d / s

800 ω B E + 1600 = 400 - 6,4 → ω B D =   - 5,2   r a d / s

As três velocidades angulares têm o sentido horário.

Passo 2

Agora vamos fazer uma análise de aceleração. A barra AB tem aceleração angular α A B = 2   r a d / s 2 , em sentido anti-horário. Vamos assumir que as acelerações angulares das outras barras têm sentido anti-horário. Analisando a aceleração na barra AB:

a → B = α → A B × r → B / A - ω A B 2 r → B / A

a → B = - 2 k → × ( - 400 i → - 800 j → ) - 4 2 ( - 400 i → - 800 j → )

a → B = - 1600 i →   + 800   j → + 6400 i → + 12800 j →

a → B = 48 00 i → + 13600 j →

Para a barra BD:

a → D = a → B + α → B D × r → D / B - ω B D 2 r → D / B

a → D =   48 00 i → + 13600 j → + α B D k → × 800 i → - 5,2 2 800 i →

a → D =   48 00 i → + 13 800 j → + 800 α B D j → -   21632 i →  

a → D =   - 168 32 i → + 800 α B D + 13 800 j →

Para a barra DE:

a → D = α → D E × r → D / E - ω D E 2 r → D / E

a → D = α D E k → × 400 i → - 500 j → - 6,4 2 ( 400 i → - 500 j → )

a → D = 500 α D E i → + 400 α D E - 16384 i → + 20480 j →

a → D = 500 α D E - 16384 i → + 400 α D E + 20480 j →

Passo 3

Agora, igualando as duas expressões para v → D , temos:

- 168 32 i → + 800 α B D + 136 00 j → = 500 α D E - 16384 i → + 400 α D E + 20480 j →

Igualando cada componente:

- 168 3 2 = 500 α B D - 16834 → α D E = - 0,896   r a d / s 2 ( s e n t i d o   h o r á r i o )

800 α B D + 13 800 = 400 - 0,896 + 20480 → α B D = 8,15 2   r a d / s 2

Resposta

  1. 8,15 rad/s²
  2. 0,896 rad/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento da barra ABC é controlado pelo movimento horizontal da haste do pistão do cilindro hidráulico D e pela guia vertical para o cursor articulado em B. Para o instante em que θ = 45 ° , a hast
Um mecanismo de avanço intermitente para fita perfurada F consiste no elemento DAB acionado pela manivela OB. O traçado do movimento do dente D é indicado pela linha tracejada. Determine o módulo da a
O mecanismo do prob 5/90 para empurrar pequenas caixas de uma linha de montagem para uma correia transportadora é apresentado com o braço OD e a manivela CB em suas posições verticais. Para a configur
O flutuador de ponta de asa retrátil é utilizado em avião capaz de pousar na água. Determine as acelerações angulars α C D , α B D e α A B no instante mostrado se a luva roscada C se desloca ao longo
Determine a aceleração angular do segmento AB se o segmento CD tem a velocidade angular e desaceleração angular mostradas.