Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 155

15.154. O pino P está preso ao colar mostrado na figura; o movimento do pino é guiado por um rasgo cortado na barra BD e pelo colar que desliza sobre a barra AE. Sabendo que, no instante considerado, as barras giram no sentido horário com velocidades angulares constantes, determine a velocidade do pino P para os dados fornecidos.

ω A E = 3,5 r a d s ,   ω b d = 2,4 r a d s

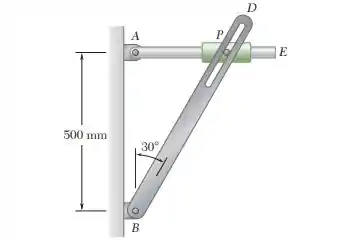
Passo 1

Vamos começar o problema destacando as informações que temos

ω A E = 3,5 r a d s ω B D = 2,4 r a d s A B - = 500   m m

Com a medida de A B - podemos determinar o tamanho de A P - e B P - .

A B - = B P - ⋅ cos ⁡ 30 °

Então

B P - = A B - cos ⁡ 30 ° = 500 cos ⁡ 30 ° = 577,35   m m

E

A P - = A B - ⋅ tan ⁡ 30 ° = 288,675   m m

Passo 2

A gente pode encontrar a velocidade no bloco P por dois métodos. No primeiro método vamos considerar P’ como o ponto que barra A E - coincide com o bloco P.

v P = v P ' + v A E

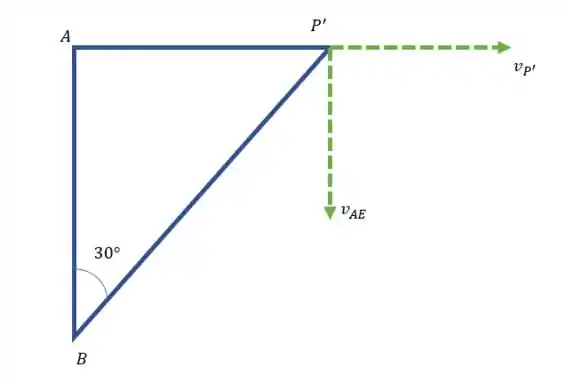
Podemos calcular v A E

v A E = A P - ⋅ ω A E

Então

v P = v P ' + A P - ⋅ ω A E

O outro modo que podemos calcular a velocidade v P é com a soma

v P = v P ' ' + v B D

O ponto P ' ' é o ponto em que a barra B D - e o bloco P coincidem.

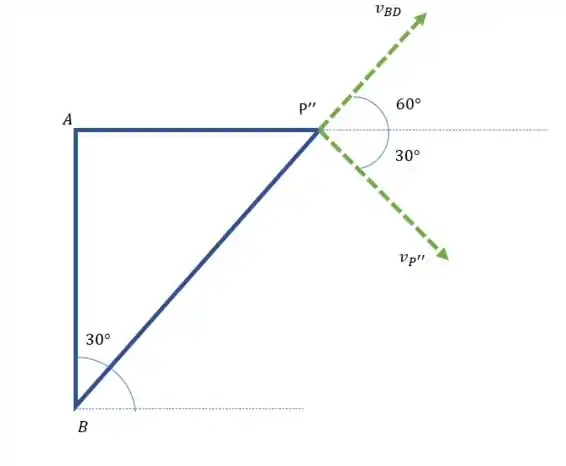
Podemos fazer

v B D = B P - ⋅ ω B D

Então

v P = v P ' ' + B P - ⋅ ω B D

Passo 3

Vamos resolver para cada componente. Na direção y   temos

- v A E = v B D ⋅ sin ⁡ 30 ° - v P ' ' ⋅ sin ⁡ 30 °

Isso fica

- A P - ⋅ ω A E = B P - ⋅ ω B D ⋅ sin ⁡ 30 ° - v P ' ' ⋅ sin ⁡ 30 °

Então

- A P - ⋅ ω A E = B P - ⋅ ω B D - v P ' ' sin ⁡ 30 °

- A P - ⋅ ω A E sin ⁡ 30 ° = B P - ⋅ ω B D - v P ' '

v P ' ' = B P - ⋅ ω B D + A P - ⋅ ω A E sin ⁡ 30 °

Substituindo os valores

v P ' ' = 577,35 ⋅ 2,4 + 288,675 ⋅ 3,5 sin ⁡ 30 °

Isso fica

v P ' ' = 3 406,365 m m s

E agora para o eixo x

v P ' = v B D ⋅ cos ⁡ 30 ° + v P ' ' ⋅ cos ⁡ 30 °

Substituindo os valores

v P ' = 577,35 ⋅ 2,4 ⋅ cos ⁡ 30 ° + 3406,365 ⋅ cos ⁡ 30 °

v P ' = 4150 m m s

Agora podemos calcular v P

v P = 4150 2 + 288,675 ⋅ 3,5 2 = 4271,22 m m s

Ou então

v P = 4,3 m s

Para descobrir a direção basta fazer

tan ⁡ θ = v A E v P '

θ = tan - 1 ⁡ 288,675 ⋅ 3,5 4150 = 13,68 °

Como podemos ver na imagem, essa velocidade está abaixo do eixo x , por tanto

θ = - 13,68 °

Resposta

  v P = 4,3 m s

θ = - 13,8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A manivela AB tem uma velocidade angular constante de 1,5 rad / s no sentido anti-horário. Para a posição mostrada, determine (a) a aceleração angular da haste BD, (b) a aceleração do colar D.
Uma corrente é enrolada em torno de duas engrenagens de 40m m de raio, que podem girar livremente em relação ao braço A B , de 320m m . A corrente move-se em torno do braço AB no sentido horário a uma
Uma corrente é enrolada em torno de duas engrenagens de 40m m de raio, que podem girar livremente em relação ao braço A B , de 320m m . A corrente move-se em torno do braço AB no sentido horário a uma
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 90 ∘ , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 60 ∘ , determine a aceleração do colar D,