Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 168
Uma corrente é enrolada em torno de duas engrenagens de de raio, que podem girar livremente em relação ao braço , de . A corrente move-se em torno do braço AB no sentido horário a uma taxa constante de relativamente ao braço. Sabendo que, na posição mostrada na figura, o braço AB gira no sentido horário em torno de a uma taxa constante , determine a aceleração de cada um dos elos indicados da corrente. Elos 1 e 2.
Passo 1
Bora pra questão 168 agora, meus caros (as)!
Bom! Temos que determinar a aceleração de cada um dos elos indicados da corrente! No caso, pra essa questão, os elos e .
O braço gira no sentido horário em torno de a uma taxa constante ... Logo, temos que...
Agora, vamos fazer um esboço dos vetores posição do nosso sistema, posicionando também os eixos de referência...
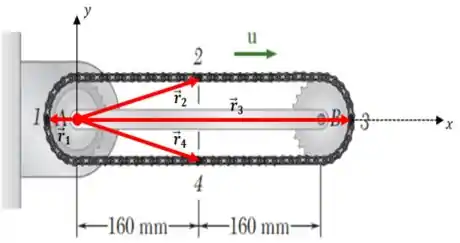
E também não podemos esquecer, é claro, da distribuição de velocidades...
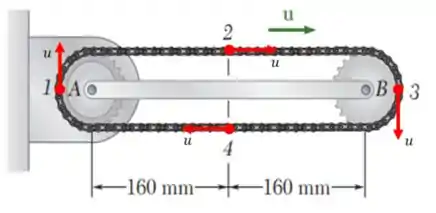
Passo 2
Para o elo , temos que...
E a velocidade de em relação à , é dada por...
Passo 3
Pois muito bem! A aceleração no elo , é dada pela seguinte fórmula.
Memoriza ela, porque a estrutura dela vale pra qualquer ponto da corrente! Agora se liga! A gente tem que vai ser dado por...
Já , que é a aceleração radial, pode ser obtido com a seguinte fórmula...
Em que é o raio das duas engrenagens, de . Logo;
Por último, só tá faltando obter ...
E então, podemos conseguir a aceleração do elo ...
Em módulo e ângulo de direção , temos que...
Passo 4
Para o elo , por sua vez, o vetor posição vai ser...
E nesse ponto, o vetor velocidade vai ficar assim...
E a fórmula pra ... Essa já tá manjada!
Por isso, primeiro vamos obter , que é dada por...
Quanto à . Como não tem engrenagem em , então não há aceleração radial...
E finalmente, só ficou faltando o :
Substituindo assim, os valores numéricos...
Obtemos ! Escrevendo em módulo e ângulo de direção...