Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 157

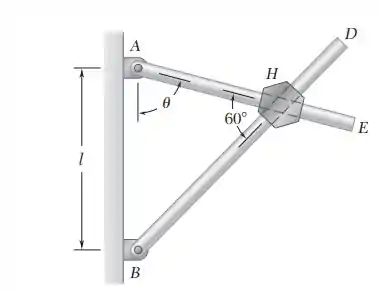
15.156. Duas barras AE e BD passam por meio de furos usinados em um bloco hexagonal. (Os furos são usinados em planos diferentes para que as barras não se toquem.) Sabendo que, no instante considerado, a barra AE gira no sentido anti-horário com uma velocidade angular constante ω , determine, para os dados fornecidos, a velocidade relativa do bloco com respeito a cada barra.

θ = 45 °

Passo 1

Vamos começar esse problema assumindo θ = 90 °

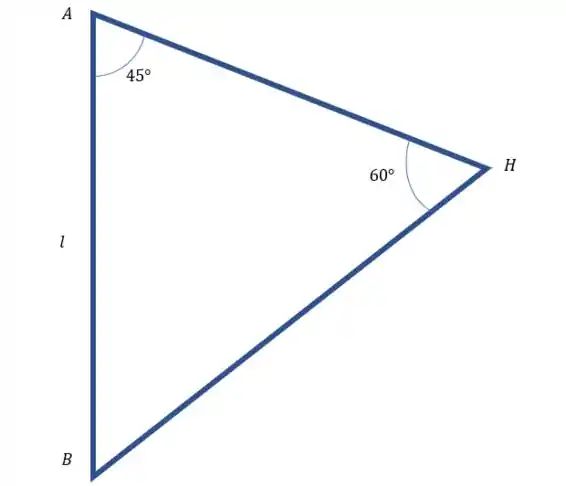
O sistema vai ficar igual a imagem aqui em cima.

Olha só, a gente tem um triângulo A H B - , e a gente sabe que um dos catetos mede l . Podemos medir as outras partes do triângulo usando as informações que temos.

Bom, a soma dos ângulos internos de um triângulo é 180°, por tanto:

Podemos usar a lei dos senos aqui

l sin ⁡ 60 ° = B H - sin ⁡ 45 ° = A H - sin ⁡ 75 °

Agora a gente pode descobrir a medida de todos os lados desse triângulo.

B H - = l sin ⁡ 45 ° sin ⁡ 60 ° = 0,8165   l    

E

A H - = l sin ⁡ 75 ° sin ⁡ 60 ° = 1,115   l

Passo 2

Beleza já temos as medidas das barras. Agora podemos calcular a velocidade do bloco H . Vamos considerar apenas a barra A H - por enquanto, podemos calcular a velocidade desse bloco assim:

v H = v H ' + v A H

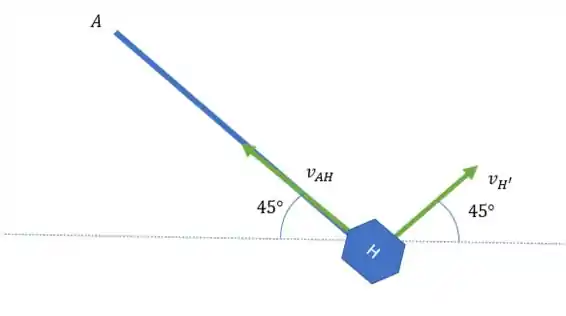
A gente pode descobrir esses ângulos através d teorema de Tales e da preposição que uma linha reta tem 180 ° .

Então temos

v H =   v A H + A H - ⋅ ω  

v H = v A H   + 1,115   l ⋅ ω

Vamos separar por componentes.

v H = - v A H ⋅ cos ⁡ 45 ° + 1,115   l ⋅ ω ⋅ cos ⁡ 45 ° i ^ + v A H ⋅ sin ⁡ 45 ° + 1,115   l ⋅ ω ⋅ sin ⁡ 45 ° j ^

Então

v H = - 0,707 ⋅ v A H + 0,707 ⋅ 1,115   l ⋅ ω i ^ + 0,707 ⋅ v A H + 0,707 ⋅ 1,115   l ⋅ ω j ^

v H = - 0,707 ⋅ v A H + 0,788 ⋅ l ω i ^ + 0,707 ⋅ v A H + 0,788   ⋅ l ω j ^

Agora vamos considerar só a barra B H -

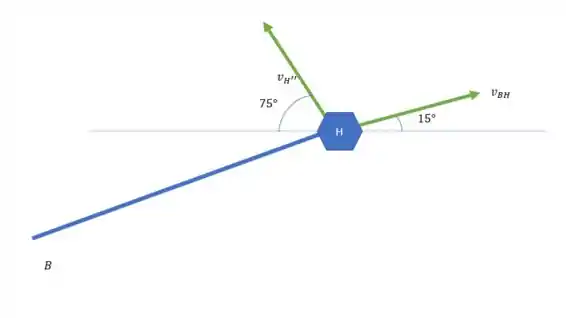
Analogamente temos

v H = v H ' ' + v B H

Então v H = B H - ⋅ ω + v B H

v H = 0,8165   l   ⋅ ω + v B H

Agora vamos separar as componentes:

v H = - 0,8165   l   ⋅ ω ⋅ cos ⁡ 75 ° + v B H ⋅ cos ⁡ 15 ° i ^ + 0,8165   l   ⋅ ω ⋅ sin ⁡ 75 ° + v B H ⋅ sin ⁡ 15 ° j ^

Isso fica

v H = 0,211 ⋅ l ω - 0,966   v B H i ^ + 0,788 ⋅ l ω + 0,259   v B H j ^

Isso vai nos dar

- 0,707 ⋅ v A H + 0,788 ⋅ l ω i ^ + 0,707 ⋅ v A H + 0,788   ⋅ l ω j ^ = 0,211 ⋅ l ω - 0,966   v B H i ^ + 0,788 ⋅ l ω + 0,259   v B H j ^

Passo 3

Vamos resolver para cada componente agora.

Na componente i ^ vai ficar assim

- 0,707 ⋅ v A H + 0,788 ⋅ l ω = 0,211 ⋅ l ω - 0,966   v B H

Vamos isolar v B H

0,966   v B H = 0,211 ⋅ l ω - 0,788 ⋅ l ω + 0,707   v A H

0,966   v B H = 0,707   v A H - 0,577 ⋅ l ω

Então

v B H = 0,732   v A H - 0,597 ⋅ l ω

Agora vamos resolver para j ^ .

0,707 ⋅ v A H + 0,788   ⋅ l ω = 0,788 ⋅ l ω + 0,259   v B H

Substituindo o valor de v B H

0,707 ⋅ v A H + 0,788   ⋅ l ω = 0,788 ⋅ l ω + 0,259   0,732   v A H - 0,597 ⋅ l ω

0,707 ⋅ v A H + 0,788   ⋅ l ω = 0,788 ⋅ l ω + 0,189   v A H - 0,155 ⋅ l ω

Vamos isolar v A H

0,707 - 0,189 v A H = - 0,155 ⋅ l ω

v A H = - 0,299 ⋅ l ω

Podemos assumir que esse é o módulo da velocidade

v A H = 0,299 ⋅ l ω

Como a gente pode ver na figura essa velocidade tem um ângulo de 45 ° com o eixo negativo de x .

Agora podemos resolver

0,966   v B H = 0,707   v A H - 0,577 ⋅ l ω

0,966   v B H = 0,707   ( - 0,299 ⋅ l ω ) - 0,577 ⋅ l ω

Isso fica

0,966   v B H = - 0,211 ⋅ l ω - 0,577 ⋅ l ω

v B H = - 0,816 ⋅ l ω

Podemos assumir o módulo também

v B H = 0,816 ⋅ l ω

E como vemos na figura, o ângulo é de 15° com o eixo positivo de x .

Resposta

v A H = 0,299 ⋅ l ω v B H = 0,816 ⋅ l ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a extremidade A da barra se desloca com uma velocidade constante v A = 6m / s , determine a velocidade angular e aceleração angular da barra e a aceleração da extremidade B no instante mostrado.
Em um dado instante, as cremalheiras têm as velocidades e acelerações mostradas. Determine a aceleração dos pontos A e B.
Em um dado instante, a engrenagem tem o movimento angular mostrado. Determine as acelerações dos pontos A e B e a aceleração angular da barra de ligação nesse instante.
A engrenagem A gira no sentido antí-horário com uma velocidade angular constante ω A = 10r a d / s , enquanto o braço DE gira no sentido horário com uma velocidade angular ω D E = 6r a d / s e uma ace
A engrenagem A é mantida fixa, e o braço DE gira no sentido horário com uma velocidade angular ω D E = 6r a d / s e uma aceleração angular α D E = 3r a d / s 2 . Determine a aceleração angular da engr