Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 131

A engrenagem A gira no sentido antí-horário com uma velocidade angular constante ω A = 10   r a d / s , enquanto o braço DE gira no sentido horário com uma velocidade angular ω D E = 6   r a d / s e uma aceleração angular α D E = 3   r a d / s 2 . Determine a aceleração angular da engrenagem B no instante mostrado.

Passo 1

Começaremos o exercício analisando a velocidade do ponto E através do diagrama a seguir:

v E = ω D E r E = 6 0,5

v E = 3   m / s

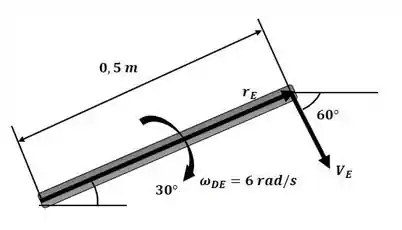
Agora iremos analisar a figura a seguir para descobrir o valor da velocidade do ponto F:

v F = ω A r F = 10 0,3

v F = 3   m / s

ω B = 15   r a d / s

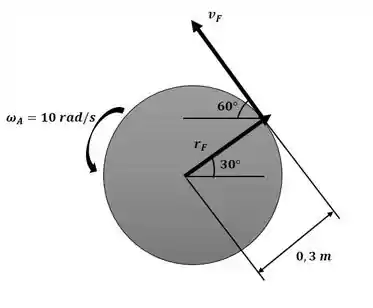
Passo 2

A localização do CI está indicado na figura a seguir, sendo assim, podemos encontrar a velocidade angular da engrenagem B:

ω B = v E r E / C I = 3 0,1

ω B = 30   r a d / s

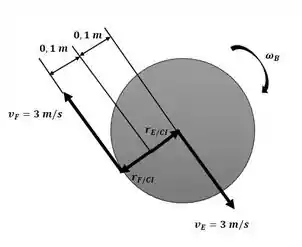
Sendo assim, podemos aplicar a equação da aceleração entre os pontos E e D ilustrados no esquema a seguir:

a → E = α D E × r → E - ω D E 2 r → E

a → E = - 3 k → × 0,5 c o s 30 ° i → + 0,5 s e n 30 ° j → - 6 2 ( 0,5 c o s 30 ° i → + 0,5 s e n 30 ° j → )

a → E = - 14,84 i → - 10,3 j →   m / s 2

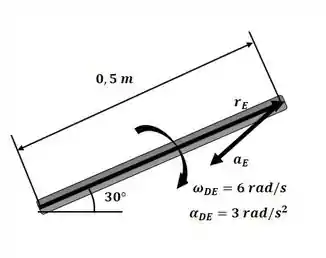
Passo 3

Agora usaremos o resultado obtido no passo 2 para aplicar a equação da aceleração entre os pontos E e F conforme a figura a seguir:

a → F = a → E + α B × r → F / E - ω B 2 r → F / E

a F c o s 30 ° i → + a F s e n 30 ° j → = ( - 14,84 i → - 10,3 j → ) + - α B k → × - 0,2 c o s 30 ° i → - 0,2 s e n 30 ° j → - 30 2 ( - 0,2 c o s 30 ° i → - 0,2 s e n 30 ° j → )

a F c o s 30 ° i → - a F s e n 30 ° j → = 141,05 - 0,1 α B i → + 0,1732 α B + 79,7 j →

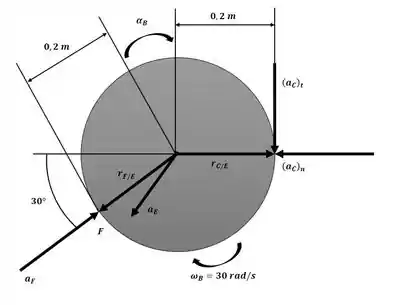
Agora, igualando os componentes:

0,866 a F = 141,05 - 0,1 α B → a F = 162,875 - 0,115 α B

0,5 a F = 0,1732 α B + 79,7

Sendo assim, substituindo o valor de a F na segunda equação:

0,5 162,875 - 0,115 α B = 0,1732 α B + 79,7

α B = 7,5   r a d / s

Resposta

α B = 7,5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O flutuador de ponta de asa retrátil é utilizado em avião capaz de pousar na água. Determine as acelerações angulars α C D , α B D e α A B no instante mostrado se a luva roscada C se desloca ao longo
Determine a aceleração angular do segmento AB se o segmento CD tem a velocidade angular e desaceleração angular mostradas.
Se a extremidade A da barra se desloca com uma velocidade constante v A = 6m / s , determine a velocidade angular e aceleração angular da barra e a aceleração da extremidade B no instante mostrado.
Em um dado instante, as cremalheiras têm as velocidades e acelerações mostradas. Determine a aceleração dos pontos A e B.
Em um dado instante, a engrenagem tem o movimento angular mostrado. Determine as acelerações dos pontos A e B e a aceleração angular da barra de ligação nesse instante.