Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 132

Se a extremidade A da barra se desloca com uma velocidade constante v A = 6   m / s , determine a velocidade angular e aceleração angular da barra e a aceleração da extremidade B no instante mostrado.

Passo 1

Com base na localização do CI, segundo a figura a seguir:

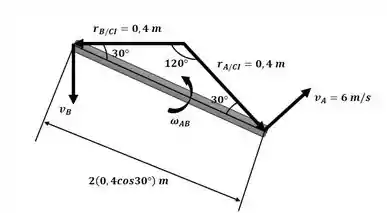
Podemos escrever:

r A / C I = r B / C I = 0,4   m

Sendo assim:

ω A B = v A r A / C I = 6 0,4 → ω A B = 15   r a d / s

E, portanto, a velocidade no ponto B é dada por:

v B = ω A B r B / C I = 15 0,4 → v B = 6   m / s

Passo 2

A magnitude da componente normal da aceleração dos pontos A e B são:

a A n = v A 2 ρ = 6 2 0,4 → a A n = 90   m / s 2

a B n = v B 2 ρ = 6 2 0,4 → a B n = 90   m / s 2

E ambas as componentes estão apontadas para o cento da trajetória circular, como será ilustrado no diagrama do passo 3. Sabemos também que v A é constante, logo a A t = 0 , e então:

a A = 90   m / s 2

Passo 3

Agora usaremos o resultado obtido no passo 2 para aplicar a equação da aceleração entre os pontos B e A conforme a figura a seguir:

a → B = a → A + α A B × r → B / A - ω A B 2 r → B / A

90 i → - a B t j → = ( - 90 c o s 60 ° i → + 90 s e n 60 ° j → ) + α A B k → × - 0,6928 c o s 30 ° i → + 0,6928 s e n 30 ° j → - 15 2 ( - 0,6928 c o s 30 ° i → + 0,6928 s e n 30 ° j → )

90 i → - a B t j → = 90 - 0,3464 α A B i → - 0,6 α A B j →

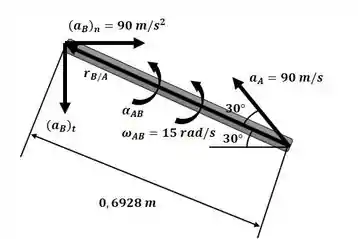
Agora, igualando os componentes:

90 = - 0,3464 α A B + 90 → α A B = 0   r a d / s 2

- a B t = - 0,6 α A B → a B t = 0   m / s 2

Dessa forma, o módulo de a B é dado por:

a B = a B t 2 + a B n 2 = 0 2 + 90 2 → a B = 90   m / s 2

E sua direção é:

θ = t g - 1 a B t a B n = t g - 1 0 90 → θ = 0 °

Resposta

α A B = 0   r a d / s 2

a B = 90   m / s 2

θ = 0 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo do Prob. 5/88 é apresentado novamente aqui. Se AO possui uma velocidade angular constante no sentido anti-horário ω O = 10r a d / s , calcule a aceleração angular da barra AB para a posiçã
A manivela giratória ED e o elemento de ligação CD obrigam a estrutura rígida ABO a oscilar em torno de O. Para o instante representado, ED e CD são ambos perpendiculares a FO, e a manivela ED possui
O mecanismo de implantação para a lança do magnetometro da nave espacial do Prob. 5/87 é novamente apresentado aqui. O elemento de acionamento OB possui uma velocidade angular constante no sentido hor
Os componentes de uma serra mecânica alternativa são apresentados na figura. A lamina de serra é montada em um arco que desliza ao longo da guia horizontal. Se o motor fira o volante a uma velocidade
Se a haste do pistão do cilindro hidráulico C tem uma velocidade constante para cima de 0,5 /s, calcule a aceleração do ponto D para a posição que θ é igual a 45 ° .