Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 128

Em um dado instante, a engrenagem tem o movimento angular mostrado. Determine as acelerações dos pontos A e B e a aceleração angular da barra de ligação nesse instante.

Passo 1

A velocidade angular da engrenagem no ponto A pode ser determinada com o auxílio da imagem a seguir:

v A = ω r A / C I = 6 ( 0,1 )

v A = 0,6   m / s

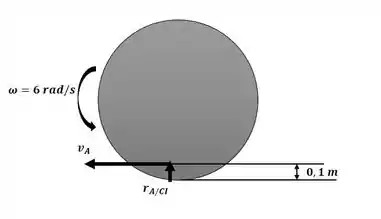
Antes de aplicar a equação da aceleração, iremos escrever as componentes de interesse:

a → O = - 12 0,3 i → = - 3,6 i →   m / s 2

r → A / O = - 0,2 j →   m

α = 12 k →   r a d / s 2

Agora iremos analisar o movimento angular dos pontos A e O através da aplicação da equação da aceleração com o auxílio da imagem a seguir:

a → A = a → 0 + α × r → A / O - ω 2 r → A / O

a → A = - 3,6 i → + 12 k → × - 0,2 j → - 6 2 ( - 0,2 j → )

a → A = 1,2 i → + 7,2 j →   m / s 2

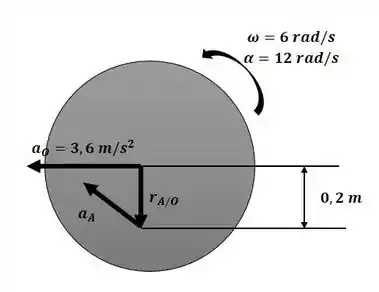
Passo 2

Agora iremos encontrar o módulo da aceleração no ponto A e a sua direção:

a A = - 1,2 2 + 7,2 2 → a A = 7,3   m / s 2

θ = t g - 1 72 12 → θ = 80,5 ° ↖

Agora iremos analisar a barra AB com o auxílio da figura a seguir:

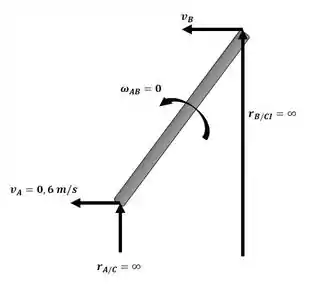
Sabendo que CI está no infinito conforme a imagem anterior, temos que:

ω A B = v A r A / C I = 6 ∞   → ω A B = 0

Passo 3

Agora iremos escrever as parcelas de interesse para aplicar a equação da aceleração:

a → B = a B i →

α A B = - α k →

r → B / A = 0,8 c o s 60 ° i → + 0,8 s e n 60 ° j →   m

Agora iremos aplicar a equação da aceleração para os pontos B e A:

a → B = a → A + α A B × r → B / A - ω 2 r → B / A

a B i → = - 1,2 i → + 7,2 j → + α A B k → × 0,8 c o s 60 ° i → + 0,8 s e n 60 ° j → - 0

Agora, igualando os componentes:

+ ↑   0 = 7,2 - 0,8 c o s 60 ° α A B → α A B = 18   r a d / s 2

+ →   a B = - 1,2 + 0,8 s e n 60 ° 18 = 11,3   m / s 2

Resposta

a A = 7,3   m / s 2

θ = 80,5 ° ↖

α A B = 18   r a d / s 2

a B = 11,3   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os componentes do dispositivo de comutação do prob. 5/85 são mostrados novamente aqui. Se a velocidade v da haste de controle é de 0,9 m/s e está diminuindo na taxa de 6 m/s² quando θ = 60 ° , determi
Se a extremidade A da barra restrita possui uma velocidade constante para eixo v A de 2 m/s quando a barra passa pela posição para qual θ = 30 ° , determine a aceleração do centro de massa G no meio d
O movimento da barra ABC é controlado pelo movimento horizontal da haste do pistão do cilindro hidráulico D e pela guia vertical para o cursor articulado em B. Para o instante em que θ = 45 ° , a hast
Um mecanismo de avanço intermitente para fita perfurada F consiste no elemento DAB acionado pela manivela OB. O traçado do movimento do dente D é indicado pela linha tracejada. Determine o módulo da a
O mecanismo do prob 5/90 para empurrar pequenas caixas de uma linha de montagem para uma correia transportadora é apresentado com o braço OD e a manivela CB em suas posições verticais. Para a configur