Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 127

Em um dado instante, as cremalheiras têm as velocidades e acelerações mostradas. Determine a aceleração dos pontos A e B.

Passo 1

A velocidade angular da engrenagem pode ser obtida usando o método da centro instantâneo de velocidade zero, da similaridade de triângulos da figura a seguir, temos:

ω = v D r D / C I   = v C r C / C I

6 r D / C I = 2 r C / C I

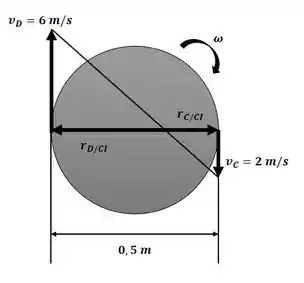
Da geometria do sistema, sabemos também que:

r D / C I + r C / C I = 0,5

Com isso, é possível encontrar os valores de r D / C I e r C / C I :

6 - r C / C I + 0,5 = 2 r C / C I → r C / C I   = 0,125   m

E agora substituindo esse valor na relação anterior:

r D / C I   = 0,375   m

Passo 2

Agora iremos analisar o movimento angular dos pontos C e D através da aplicação da equação da aceleração com o auxílio do esquema a seguir:

a → D = a → C + α × r → D / C - ω 2 r → D / C

64 i → + 2 j → = - 64 i → - 3 j → + - α k → × - 0,5 i → - 16 2 ( - 0,5 i → )

64 i → + 2 j → = 64 i → + 0,5 α - 3 j →

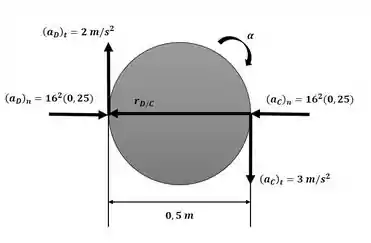
Igualando as componentes na direção j:

2 = 0,5 α - 3 → α = 10   r a d / s 2

Agora iremos obter a aceleração no ponto A analisando o movimento angular nos pontos A e C com o auxílio da figura a seguir:

a → A = a → C + α × r → A / C - ω 2 r → A / C

a → A = - 64 i → - 3 j → + - 10 k → × - 0,25 i → - 16 2 ( - 0,25 i → )

a → A = 0,5 j → = 0,5   m / s 2 ↓

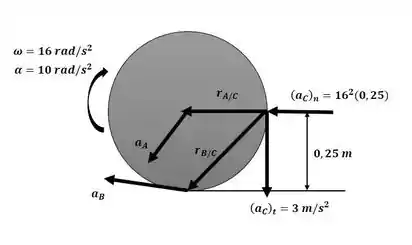
Passo 3

Agora podemos obter a aceleração do ponto B analizando o movimento angular nos pontos B e C, ainda com o auxílio da imagem do passo 2:

a → B = a → C + α × r → B / C - ω 2 r → B / C

a → B = - 64 i → - 3 j → + - 10 k → × - 0,25 i → - 0,25 j → - 16 2 ( - 0,25 i → - 0,25 j → )

a → B = - 2,5 i → + 63,5 j →   m / s 2

Sendo assim, a magnitude e a direção da aceleração no ponto B são dados por:

a C = - 2,5 2 + 63,5 2 = 63,5   m / s 2

θ = t g - 1 63,5 2,5 = 87,7 ° ↖

Resposta

a A = 0,5   m / s 2 ↓

a C = 63,5   m / s 2

θ = 87,7 ° ↖

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por um curto intervalo de movimento, a barra AO possui uma velocidade angular constante ω = 4 r a d / s . Determine a aceleração angular α A B da barra AB para o instante em que AO esta paralela ao ei
Se a barra AB do mecanismo de quatro barras possui uma velocidade angular constante no sentido anti-horário de 40 rad/s durante um intervalo que inclui o instante representado, determine a aceleração
O mecanismo do prob 5/118 é reapresentado aqui, onde a tira flexível F presa ao setor E recebe uma velocidade constante de 4 m/s conforme mostrado. Para o instante em que BD este perpendicular a AO, d
No projeto desse mecanismo, o movimento da placa quadrada é controlado pelas duas barras articuladas. A barra AO possui uma velocidade angular constante ω = 4 r a d / s durante um curto intervalo de m
16.97. A unidade de bombeamento de petróleo consiste de um balancim A B , a barra de conexão B C e a manivela C D . Se a manivela gira com uma taxa constante de 6 r a d / s , determine a velocidade da