Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 156

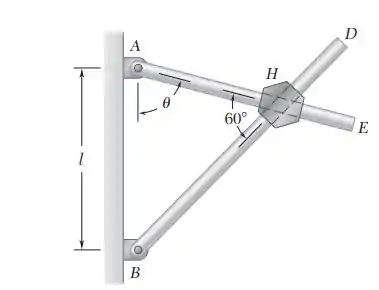
15.156. Duas barras AE e BD passam por meio de furos usinados em um bloco hexagonal. (Os furos são usinados em planos diferentes para que as barras não se toquem.) Sabendo que, no instante considerado, a barra AE gira no sentido anti-horário com uma velocidade angular constante , determine, para os dados fornecidos, a velocidade relativa do bloco com respeito a cada barra.

Passo 1

Vamos começar esse problema assumindo

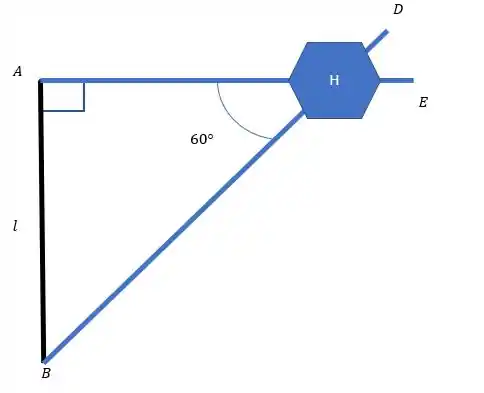
O sistema vai ficar igual a imagem aqui em cima.

Olha só, a gente tem um triângulo , e a gente sabe que um dos catetos mede . Podemos medir as outras partes do triângulo usando as informações que temos.

Bom, a soma dos ângulos internos de um triângulo é 180°, por tanto:

Podemos dizer então que

Então

E também podemos dizer que

Então

Passo 2

Beleza já temos as medidas das barras. Agora podemos calcular a velocidade do bloco . Vamos considerar apenas a barra por enquanto, podemos calcular a velocidade desse bloco assim:

A gente ainda não pé capaz de dizer exatamente o sentido de , mas vamos deixar o vetor desenhado só para ilustrar o problema.

Então temos

Isso fica

Agora vamos considerar só a barra

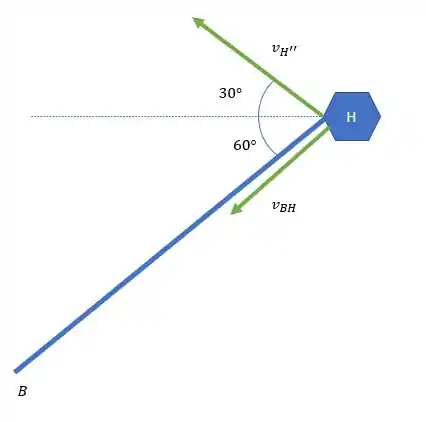
Analogamente temos

A gente consegue determinar o ângulo de da velocidade porque essa velocidade tem que ser perpendicular a barra .

Temos então

Agora vamos separar as componentes:

Isso fica

Isso vai nos dar

Passo 3

Vamos resolver para cada componente agora.

Na componente vai ficar assim

Vamos isolar

Só tem um resultado possível para isso

Esse resultado vai facilitar bastante.

Agora vamos fazer para a componente

Ou seja

Viu como facilitou? E simples assim temos a resposta do item (a). Agora vamos para o item (b).

Passo 4

No item (b) as coisas vão ficar um pouquinho mais complicadas, agora temos , então nosso desenho fica:

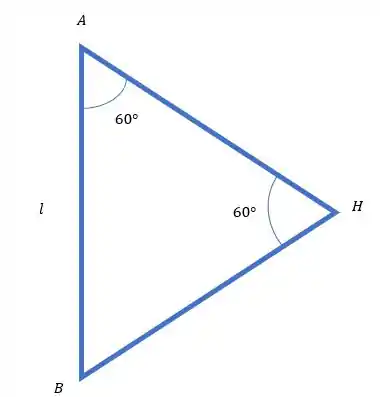
Olha só, nosso triângulo tem dois ângulos de 60°. Sabe o que isso significa? É um triângulo equilátero, todos os lados do triângulo têm a mesma medida, isso vai ser bem útil pra gente!

Vamos usar o mesmo raciocínio que usamos no item (a). Começando com a barra .

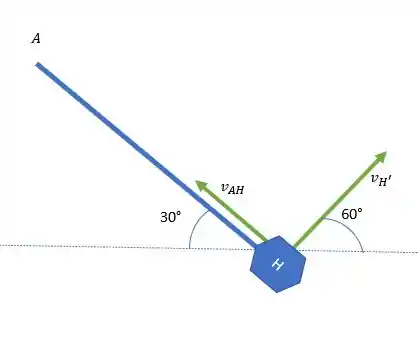
A gente descobre o ângulo usando duas preposições. A primeira é que o sistema de coordenas é aquele que o eixo corta a barra exatamente ao meio, e a segunda é que uma linha reta tem 180°.