Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 114

As extremidades da barra AB estão confinadas a se deslocarem ao longo das trajetórias mostradas. Em um dado instante, A tem uma velocidade de 2,4 m/s e uma aceleração de 0,9 m/s². Determine a velocidade angular e a aceleração angular de AB nesse instante.

Passo 1

Começaremos o exercício calculando a velocidade angular da haste AB através da velocidade no ponto A e o seu comprimento:

ω = v A l = 2,4 1,2 → ω = 2   r a d / s

Passo 2

Agora iremos calcular o valor da velocidade e da aceleração normal em B:

v B = ω r = 2 2,4 → v B = 4,8   m / s

E a aceleração ilustrada na figura a seguir é dada por:

a B n = v B 2 l = 4,8 2 1,2 → a B n = 19,2   m / s 2

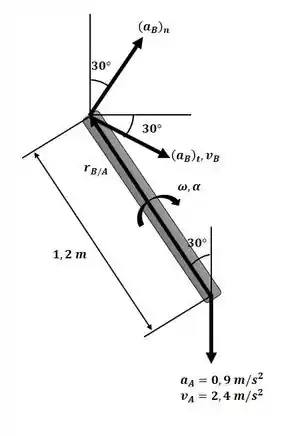
Passo 3

Agora podemos escrever a equação da aceleração em função das suas componentes, baseando-se no diagrama apresentado no passo 2:

a → B = a → A + a → B / A

+ →   19,2 s e n 30 ° + a B t c o s 30 ° = 0 + α 1,2 s e n 60 ° + 2 2 ( 1,2 ) c o s 60 °

a B t = 1,2 α

Essa será nossa equação 1.

+ ↑   19,2 c o s 30 ° - a B t s e n 30 ° = - 0,9 + α 1,2 c o s 60 ° - 2 2 ( 1,2 ) s e n 60 °

Essa será nossa equação 2. Agora substituindo o valor encontrado na equação 1 nessa última equação, temos:

19,2 c o s 30 ° - ( 1,2 α ) s e n 30 ° = - 0,9 + α 1,2 c o s 60 ° - 19,2 s e n 60 °

α = 18,07   r a d / s 2

Resposta

ω = 2   r a d / s

α = 18,07   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração do ponto C é de 0,5 m/s² para baixo e a aceleração angular da viga é de 0,8 rad/s² no sentido anti-horário. Sabendo que, no instante considerado, a velocidade angular da viga é nula, dete
A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a
Um carro C é suportado por um rodízio A e um cilindro B, cada um com 50 mm de diâmetro. Sabendo que no instante mostrado na figura o carro tem uma aceleração de 2,4 m/s² e uma velocidade de 1,5 m/s, a
Um automóvel desloca-se para a esquerda a uma velocidade constante de 80 km/h. Sabendo que o diâmetro da roda é de 500 mm, determine a aceleração (a) do ponto B, (b) do ponto C, (c) do ponto D.
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s², ambas orientadas para ci