Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 159
O mecanismo de retorno rápido consiste da manivela e do braço com ranhura . Se a manivela gira com a velocidade angular e a aceleração angular no instante mostrado, determine a velocidade angular e a aceleração angular de nesse instante.
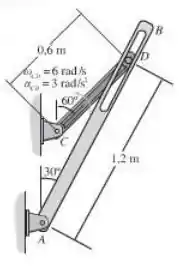
Passo 1
Como o mecanismo em questão possui uma conexão através do ponto , é possível encontrar as informações de velocidade e aceleração neste ponto do bloco deslizante e, então, fazer a análise da parte do membro com ranhura para aproveitar a transmissão da velocidade e da aceleração de um ponto ao outro.
Então, a velocidade de em relação a será dada por:
E a aceleração de em relação a é:
Onde:
velocidade angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem;
aceleração angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem.
Passo 2
Fazendo o diagrama de corpo livre (DCL) do mecanismo todo:
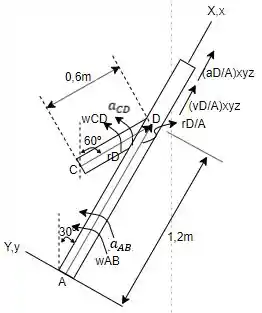
O vetor posição de até , , que será:
E o vetor posição de até , é dado por:
Analisando a manivela , como ela está fixa em um ponto e gira em torno dele, a velocidade e a aceleração do ponto poderão ser dados por:
E:
Logo:
Passo 3
Sendo assim, tendo essas variáveis determinadas juntamente com os valores previamente fornecidos pelo exercício, se torna possível fazer o cálculo dos valores desejados do membro fazendo a análise relativa entre os pontos e .
Portanto, aplicando a outra equação da velocidade em , tem-se:
Tal que a velocidade angular da referência medida a partir do referencial será a soma das velocidades angulares agindo sobre o membro , ou seja:
E, similarmente, a aceleração angular da referência medida a partir do referencial será a soma das acelerações angulares agindo sobre o membro dado por:
Sendo assim, voltando a equação da velocidade em :
Separando as variáveis por eixo do sistema de referência, obtém-se:
E
Passo 4
Agora, para determinar a aceleração deve-se aplicar a equação:
Dessa forma, será obtido:
Resolvendo as somas e produtos vetoriais:
Novamente, separando as variáveis por eixo do sistema de referência, obtém-se:
E: