15.219. Mecanismo do Problema 15.207.

Passo 1
No problema 15.207 a gente tem um sistema mais ou menos assim:
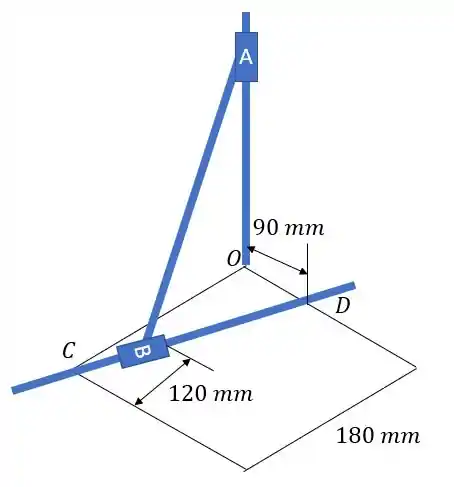
E o colar B se aproxima do ponto D a uma velocidade de .
Nesse problema estamos interessados no colar .
Passo 2
Vamos começar reunindo informações, primeiro vamos determinar o vetor distância de cada ponto:
Com essas informações a gente pode determinar , que vai ser importante, mas primeiro vamos ter que calcular várias outras posições, vamos lá!
Podemos começar com:
Então
Esse resultado vai ajudar a gente a calcular outra distância:
E agora a gente vai calcular outra distância:
Então
A gente está quase chegando no que a gente quer
Então
Passo 3
A gente calculou porque a gente já sabe o valor do módulo desse vetor. Lá no enunciado do problema 15.207 a gente descobre que , então a gente tem tudo para determinar o valor de .
Vamos resolver para .
E agora a gente pode continuar procurando a aceleração de A em paz, porque agora temos uma informação poderosa:
Passo 4
E agora que calculamos todas as posições que precisamos, vamos calcular todas as velocidades que precisamos, começando com:
A gente já sabe todos esses valores, é só substituir
E agora vamos calcular a velocidade no colar A. Sabemos:
E também que
Opa... a gente ainda não sabe . Mas olha só que coisa interessante! são perpendiculares a , ou seja:
Então se fizermos
A gente chega em
Mas como
Então
A gente sabe que só tem componente em , então:
E daqui temos que
Logo
Isso significa que
E com isso podemos calcular uma velocidade interessantíssima para nós:
Isso fica
Passo 5
Finalmente vamos chegar ao ponto do problema, a aceleração. Bom, podemos dizer que
E que
Para calcular podemos usar a relação:
Sabemos que , então vamos nos concentrar em .
O truque aqui é enxergar dois vetores paralelos, que nesse caso são e , então
Então, usando a relação
Vamos chegar em
Então se fizermos
Então teremos
E aí vamos chegar numa equação final:
Então temos
Então
Então a resposta do problema é