Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 48

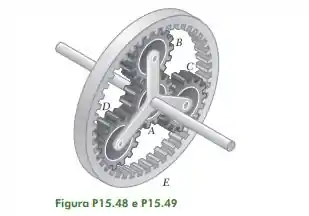
15.49. No sistema de engrenagens planetárias mostrado na figura, o raio da engrenagem central A é a, o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a +-2b. A velocidade angular da engrenagem A é A no sentido horário e a engrenagem externa é estacionária. Se a velocidade angular do suporte BCD deve ser A/5 no sentido horário, determine (a) o valor requerido da razão b/a, (b) a velocidade angular correspondente de cada engrenagem planetária.

Passo 1

Vamos começar mais outra.

A situação que a gente tem é parecida com esse desenho:

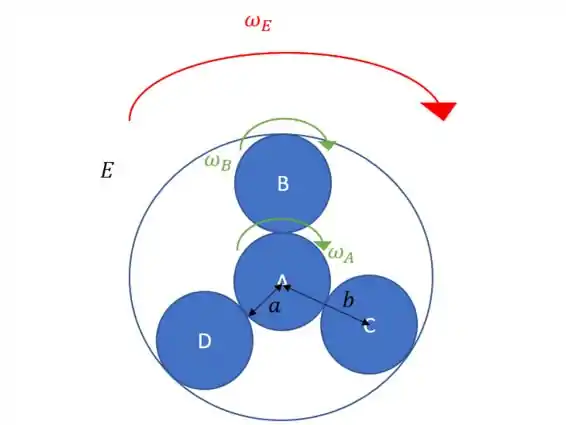
Nós podemos fazer o seguinte:

v A = a ⋅ ω A

E a velocidade do suporte é

v S = a + b ω S

Mas a velocidade do suporte também é a velocidade que o centro das engrenagens B,C e D estão girando em relação ao centro.

v B ' = v S

E sabemos que

v B ' = v A + v B

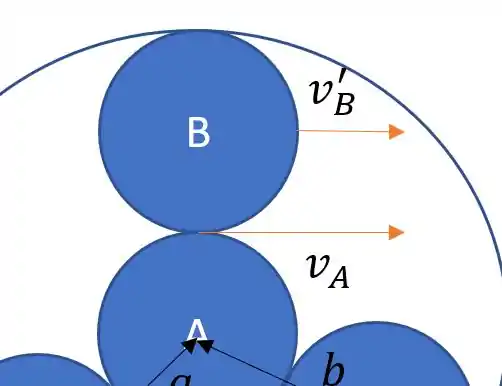
Então

a + b ω S = v A + v B

Ou ainda

a + b ω S = a ω A + b ω B

E também podemos fazer

v E = a + 2 b ω E

Mas existe outro jeito para calcularmos v E :

v E = v B ' + v B

Então

v B ' + v B = a + 2 b ω E

Ou

a + b ω S + b ω B = a + 2 b ω E

Passo 2

Se somarmos

a + b ω S = a ω A + b ω B

E

a + b ω S + b ω B = a + 2 b ω E

Ficamos com

2 a + b ω S = a ω A + a + 2 b ω E

Então

ω S = a ω A + a + 2 b ω E 2 a + b

Mas do enunciado sabemos que

ω E = 0

E

ω S = 1 5 ω A

Então

1 5 ω A = a ω A 2 a + b

Podemos cortar ω A

1 5 = a 2 a + b

E isso aqui fica

2 5 a + b = a  

a + b = 5 2 a

Podemos dividir tudo por a

1 + b a = 5 2

Então

b a = 5 2 - 1 = 3 2

Passo 3

Agora vamos para o item (b). Vamos novamente usar as equações:

a + b ω S = a ω A + b ω B

E

a + b ω S + b ω B = a + 2 b ω E

Mas agora vamos subtrai-las

2 b ω B = a + 2 b ω E - a ω A

Então

ω B = a + 2 b ω E - a ω A 2 b

Usando

ω E = 0

Temos

ω B = - a ω A 2 b

Isso é

ω B = - a b ω A 2  

Mas sabemos que

b a = 3 2

Então

a b = 2 3

Logo

ω B = - 2 3 ω A 2 = - ω A 3

Resposta

a : b a = 3 2

b : ω B = - ω A 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/93) Para o instante representado , o vértice A da placa retangular possui uma velocidade v A = 2,8m / s e a placa possui uma velocidade angular no sentido horário ω = 12 r a d / s . Determine o módu
5/106) A lâmina de um cortador de grama motorizado gira no sentido nti-horário na velocidade angular de 1800r p m . Se o centro do do corpo é um círculo de raio 0,75m m , calcule a velocidade v O do c
5/98) Um mecanismo de automóveis “conduz”dois conjuntos de roda e pneu por um piso horizontal como apresentado . Ele anda com velocidade constante v e mantém os pneus na configuração indicada com a me
5/97) Em um determinado instante o vértice B da placaem mformato de triângulo retângulo possui uma velocidade de 200m m / s nadireção mostrada . Se o cento instantâneo da velocidade nula para a placa
5/99) O mecanismo é retratado aqui na escala indicada . Para aposição apresentada , a barra O 1 A possui uma velocidade angular no sentido horário de 4r a d / s . Por medida direta a partir da figura