Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 32

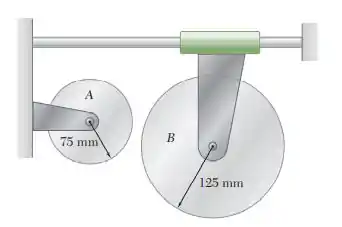
O disco B encontra-se em repouso quando é posto em contato com o disco A , que está girando livremente a 450   r p m   no sentido horário. Após 6   s de deslizamento, período em que cada disco assume uma aceleração angular constante, o disco A atinge uma velocidade angular final de 140   r p m no sentido horário. Determine a aceleração angular de cada disco durante o período de deslizamento.

Passo 1

Fala aí, galera. Tudo certo? Bora fazer mais questões. Neste problema, temos que determinar a aceleração angular de cada disco durante o período de deslizamento.

Sabemos a velocidade inicial e a velocidade após 6 s do disco A . Logo, vamos utilizar a relação para movimento circular uniformemente variável, temos que a aceleração angular no instante t = 6 s é dada por:

ω A = ω A 0 + α A t 140   r p m = 450   r p m + α A t 6

Vamos passar as velocidades de r p m para r a d / s . Com isso, temos:

14,661   r a d / s = 4 7,124   r a d / s + α A t 6 α A = - 5,41   r a d / s 2

Passo 2

Agora, para determinarmos a aceleração angular no disco B durante o período de deslizamento, vamos utilizar a relação que nos diz que as velocidades v A e v B são iguais em módulo, logo:

v A = v B ω A r A = ω B r B

Substituindo:

- 5,41 0,075 = ω B 0,125 ω B = 8,796   r a d / s

Com a velocidade angular encontrada, basta utilizarmos a seguinte relação para determinarmos a aceleração angular:

ω B = ω B 0 + α B t 8,796 = 0 + α B 6 α B = 1,466   r a d / s 2

Isso é tudo, pessoal. Bora praticar mais!

Resposta

α A = - 5,41   r a d / s 2

α B = 1,466   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema de amostra 18.6 assumindo que o meteorito ataca p satélite em C com velocidade inicial v θ = ( 2000 m / s ) i
Uma moeda é lançada ao ar. Observa-se girar a uma taxa de 600 rpm em torno de um eixo GC perpendicular à moeda e processar em torno da direção vertical GD. Sabendo que GC forma um ângulo de 15° com GD
Um cubo sólido do lado c = 120 mm é preso como mostrado a um cabo AB de comprimento 240 mm. O cubo gira em torno de sua diagonal BC e processa em torno do eixo vertical AD. Sabendo que θ = 25 ∘ e β =
Um registro fotográfico de alta velocidade mostra que um determinado projétil foi disparado com uma velocidade horizontal V de 600 m / se com seu eixo de simetria formando um ângulo β = 3 ∘ com a hori
Uma placa retangular homogênea de massa nos lados c e 2c é mantida em A e B por um eixo com extremidade em garfo de massa desprezível, que é suportado por um rolamento em C. A placa está livre para gi