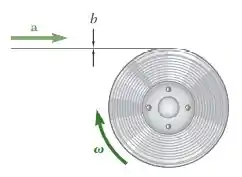
Uma fita de vídeo está sendo rebobinada em um carretel VCR que gira a uma velocidade constante de . Representando por o raio do carretel em um dado instante qualquer e por a espessura da fita, deduza uma expressão para a aceleração da fita ao se aproximar do carretel.

Fala aí, galera. Tudo certo? Bora fazer mais questões de Mecânica pra ficar craque. Este problema nos pede para determinarmos uma expressão para a aceleração angular da fita ao se aproximar do carretel.

Para isso, ele nos fornece algumas informações. A velocidade do rolo é constante e é representada por , e a espessura do papel por . Com isso, quando uma camada de fita é enrolada e seja a velocidade da fita:

E também:

Assim, teremos que a variação do raio em função do tempo, ou seja, no desenrolar do rolo de papel vai ser:

Sabemos também que a aceleração angular é dada pela derivada em função do tempo da velocidade angular. Logo, para o carretel, temos:

Substituindo:

Isso é tudo, pessoal. Bora praticar mais!