Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 59

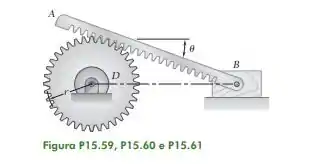
15.59. Uma cremalheira reta repousa sobre uma engrenagem de raio r e está presa ao bloco B como mostra a figura. Representando por D a velocidade angular horária da engrenagem D e por o ângulo formado pela cremalheira e a horizontal, deduza expressões para a velocidade do bloco B e para a velocidade angular da cremalheira em termos de r, e D.

Passo 1

A gente pode começar essa questão determinando a velocidade no dente da engrenagem D.

v D ' = r ⋅ ω D

Outra coisa que podemos fazer é determinar o tamanho D ' B

l = r tan ⁡ θ

Passo 2

Podemos fazer agora

E desenhando o diagrama de velocidades

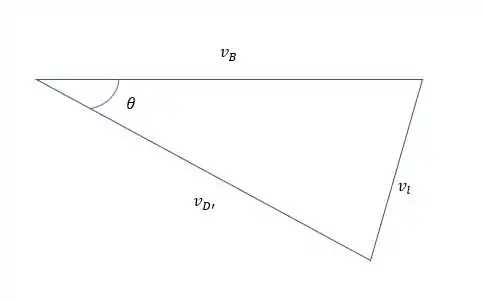
Nesse triangulo podemos ver as relações

v B = v D ' cos ⁡ θ = r ω D cos ⁡ θ

Essa é a velocidade do bloco B em termos de r ,   θ e ω D .

E também podemos tirar a relação

v l = v D ' tan ⁡ θ = r ω D tan ⁡ θ

Passo 3

Bom, agora vamos definir a velocidade angular da cremalheira. De acordo com a imagem temos:

l ω A B = v l

Então

l   ω A B = r ω D tan ⁡ θ

Logo

ω A B = r ω D tan ⁡ θ l

Resposta

v l = v D ' tan ⁡ θ = r ω D tan ⁡ θ ω A B = r ω D tan ⁡ θ l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.88. A roda gira sobre seu cubo sem deslizar na superfície horizontal. Se a velocidade do centro da roda é V c = 0,6 m s , para a direita, determine as velocidades dos pontos A e B no instante mostr
16.95. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8m / s e V E = 3 m / s . Demonstre que é necessário que a roda deslize
72. O trem de engrenagens epicicloidal consiste da engrenagem sol A que está engrenada à engrenagem planetária B. Esta tem um cubo interior com a engrenagem C que está fixo em B e engrenado na engrena
73. Se a barra de ligação AB tem uma velocidade angular ω A B = 4r a d / s no instante mostrado, determine a velocidade do bloco deslizante E nesse instante. Também identifique o tipo de movimento de
16.106. A placa quadrada está restringida dentro das ranhuras em A E B . Quando θ = 30 ° , o ponto A está se deslocando com V A = 8 m s . Determine a velocidade do ponto C nesse instante.