Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 95
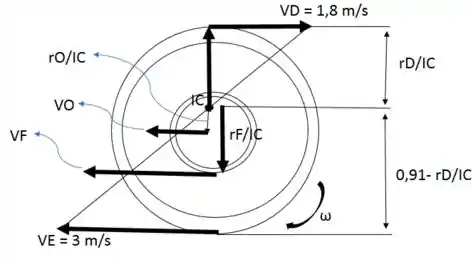
16.95. A roda está rigidamente fixada à engrenagem , que está engrenada às cremalheiras e Se tem uma velocidade e . Demonstre que é necessário que a roda deslize sobre o trilho fixo Também determine a velocidade angular da engrenagem e a velocidade de seu centro
Passo 1
Movimento Geral do Plano: A localização do pode ser encontrada usando o
triângulos mostrados na Fig ele será a linha que intercepta os demais segmentos:
Passo 2
Através dos dados e da figura obtida, podemos determinar o segmento de linha para com relação a através da semelhança de triângulos que a figura nos dar:
=
=
=
Passo 3
Para encontrarmos o valor de em relação a teremos que calcular a diferença entre os segmentos que o intercepta, neste caso, usaremos as dimensões da figura original do livro, essas medidas equivalem a:
=
=
Passo 4
Como no caso anterior, iremos determinar o valor do segmento de linha para com relação ao ponto , portanto teremos que calcular a soma das dimensões dada a engrenagem e calcular a diferença entre o ponto , Logo:
=
=
=
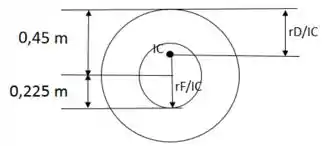
Passo 5
Assim, a velocidade angular da engrenagem é dada com a relação entre a velocidade em e seu respectivo segmento de linha, onde:
= =
=
Passo 6
A velocidade do ponto de contato entre a roda e a pista é dada a partir da a velocidade angular da engrenagem pelo segmento de linha pois irão atribuir na sua velocidade, logo:
= .
=
=
Sendo 0, a roda escorregou na pista.
Passo 7
A velocidade do ponto O da engrenagem porém, dependerá somente da velocidade angular da engrenagem, e do ponto central da mesma:
= .
=
=
Resposta
=
=