Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 72
72. O trem de engrenagens epicicloidal consiste da engrenagem sol A que está engrenada à engrenagem planetária B. Esta tem um cubo interior com a engrenagem C que está fixo em B e engrenado na engrenagem interna R. Se a barra de ligação DE conectada por pino em B e C está girando a em torno do pino E, determine as velocidades angulares das engrenagens satélites e sol.
Passo 1
Um esboço que pode ajudar na resolução do problema pode ser representado por:
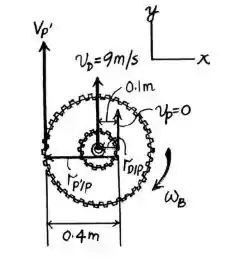
Passo 2
Do seguimento DE, temos que:
Passo 3
Utilizando a equação da velocidade relativa, temos que:
Passo 4
Adodando um ponto P´ como sendo um ponto de contato, podemos escrever:
Resposta
Exercícios de Livros Relacionados
5/77) A manivela O A oscila em torno da posição θ = 0 obrigando C B , por sua vez , a oscilar . Se O A possui uma velocidade angular no sentido anti-horário de 6r a d / s quando θ = 30 ° , determine a
5/70) O disco circular rola sem deslizar com uma velocidade angular no sentido horário ω = 4r a d / s . Para o instante representado , escreva as expressões vetoriais para a velocidade de A com relaçã
5/75) Cada uma das barras deslizantes A e B se acopla na sua borda respectiva das duas rodas rebitadas sem deslizar . Determine o módulo da velocidade do ponto P para a posição indicada.
5/72) No instante representado , a velocidade do ponto A da barra de 1,2m é de 3m / s para a direita . Determine a velocidade v B do ponto B e a velocidade angular ω da barra . O diâmetro das pequenas
5/73) A unidade em A consiste em um motor com redução de alto torque que gira a barra A B na taxa constante θ ' = 0,5r a d / s . A unidade A é livre para se mover ao longo da superfície horizontal . D