Passo 1
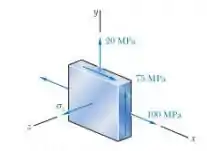
E ai gurizada tudo bem? O enunciado pede que a gente determine o intervalo de valores de para o qual não ocorre o escoamento. Vamos lá então :D
Passo 2
Temos que , então vamos dar continuidade ;)

E ai gurizada tudo bem? O enunciado pede que a gente determine o intervalo de valores de para o qual não ocorre o escoamento. Vamos lá então :D
Temos que , então vamos dar continuidade ;)