Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 60

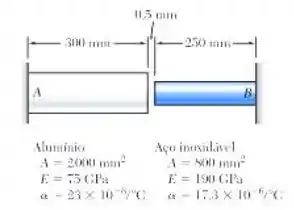
Na temperatura ambiente (20°C) existe um espaçamento de 0,5 mm entre as extremidades das barras mostradas na figura. Algum tempo depois, quando a temperatura atingir 140°C, determine (a) a tensão normal na barra de alumínio e (b) sua variação do comprimento.

Passo 1

Fala ai gurizada tudo belezinha? Para determinarmos a tensão normal na barra de alumínio, primeiramente temos que determinar a variação de temperatura do elemento que é dada por:

∆ T = 140 - 20 = 120 ° C

Expansão térmica livre é obtida através da equação:

δ T = L a α a   x   ∆ T + L s α s   x   ∆ T = 0,300   x   23   x   10 - 6   x   120 + 0,250   x   17,3   x   10 - 6   x   120 = 1,347   x   10 - 3 m

Encurtamento devido a carga P é obtido como apresentado abaixo:

δ P = 1,347   x   10 - 3 - 0,5   x   10 - 3 = 0,847   x   10 - 3 m   δ P = P L a E a A a + P L s E s A s = L s E a A a + L s E s A s P = 0,300 75   x   10 - 9   x   2000   x   10 - 6 + 0,250 190   x   10 - 9   x   800   x   10 - 6   P = 3,6447   x   10 - 9 P

Igualando, podemos achar P: = 3,6447   x   10 - 9 P = 0,847   x   10 - 3 P = 232,39     x   10 3 N

Passo 2

Agora sim podemos determinar a tensão e a variação do comprimento respectivamente:

  1. σ a = - P A a = - 232,39   x   10 3   2000   x   10 - 6 = - 116,2   x   10 6 P a    
  2. δ a = L a α a   x   ∆ T - P L a E a A a

δ a = 0,300   x   23   x   10 - 6   x   120 - 232,39   x   10 3   x   ( 0,300 ) 75   x   10 9   x   ( 2000   x   10 - 6 )     = 363   x   10 - 6 m  

Resposta

  1. σ a = - 116,2   M P a
  2. δ a = 0,363   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tira de latão AB foi presa a um suporte fixo em A e apoia-se sobre um suporte rugoso em B. Sabendo que o coeficiente de atrito é 0,60 entre a tira de latão e o suporte B, determine o decréscimo na t
O corpo de prova de alumínio mostrado está submetido a duas forças iguais axiais, opostas e centradas de intensidade P, (a) sabendo que E = 70G P aeσ a d m = 200M P a , determine o máximo valor admiss
A montagem mostrada consiste em uma casca de alumínio ( E a = 106x10 6 p s i ,α = 12,9x10 - 6 / ° F ) completamente colada ao núcleo de aço ( E = 29x10 6 p s i , α s = 6,5x10 - 6 / ° F ) e não tension
Um poste de concreto de 4ft é reforçado por quatro barras de aço, cada uma com um diâmetro de ¾ in. Sabendo que E S = 29x10 - 6p s ieE S = 3,6x10 6 p s i , determine a tensão normal no aço e no concre
O fio uniforme ABC, de comprimento 2l quando não esticado, é preso aos suportes mostrados na figura de lhe é aplicada uma força vertical P no ponto médio B. Designando por A a área da seção transversa