Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 88

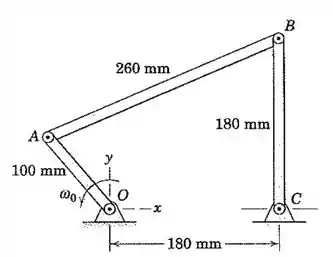
No mecanismo de quatro barras mostrado, a haste de controle AO possui uma velocidade angular no sentido anti-horário ω O = 10 r a d / s durante um curto intervalo de movimento. Quando a haste CB ultrapassa a posição vertical mostrada, o ponto A possui as coordenadas x=-60 mm e y=80 mm. Determine por meio da álgebra vetorial as velocidades angulares de AB e BC.

Passo 1

Esta é mais uma questão de mecanismo. Muito importante neste tipo de questão é fazer um esboço mostrando todos os vetores posição e velocidade. Vamos começar com o que nos foi dado pelo enunciado e pela Figura:

- Velocidade angular de AO: ω O = 10   r a d / s , sentido AH

- O vetor posição da haste AO: r A O → = - 0,06   i ^ + 0,08   j ^

- O vetor posição da haste BC: r B C → = 0,18   j ^

Os pontos A e B, por estarem em barras fixas articuladas, apresentam suas velocidades na direção perpendicular às barras AO e BC, respectivamente. Outro dado que será muito importante nesta questão é a velocidade relativa V A / B , por ser o elemento que une as barras fixas. Lembrando que a velocidade relativa possui direção perpendicular à barra AB.

Passo 2

Vamos começar a desenvolver o problema. Como dito anteriormente, é muito importante fazer um esboço com os vetores dados, pois isso facilitará muito a visualização da questão. Vamos a ele:

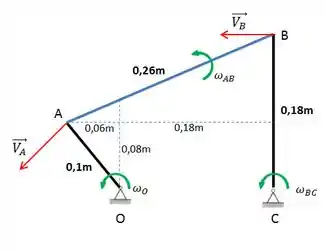
A partir do esboço, podemos escrever o vetor posição r A B :

r A B → = - 0,18 + 0,06 i ^ - 0,18 - 0,08 j ^ = - 0,24 i ^ - 0,10 j ^

Agora que já calculamos todos os vetores posição, podemos calcular as velocidades.

V A → = ω O   k ^ × r A O → = 10 k ^ × ( - 0,06   i ^ + 0,08   j ^ )

V A → = - 0 , 8 i ^ - 0,6 j ^   m / s

V B → = ω B C   k ^ × r B C → = ω B C k ^ × 0,1 8   j ^

V B → = - 0,18 ω B C   i ^   m / s

V A / B → = ω A B   k ^ × r A B → = ω A B k ^ × ( - 0,24 i ^ - 0,10 j ^ )

V A / B → = 0,1 ω A B   i ^ - 0,24 ω A B j ^   m / s

Passo 3

Bom, nesta etapa iremos calcular as velocidades angulares. Para isto, precisamos relacionar as velocidades de A e B com a velocidade relativa. Para isso usamos a equação:

V A = V B + V A / B

Substituindo os valores:

- 0,8 i ^ - 0,6 j ^ = - 0,18 ω B C   i ^   + 0,1 ω A B   i ^ - 0,24 ω A B j ^  

Para melhorar a visualização e os cálculos, vamos decompor a equação acima nas direções i ^   e   j ^ :

- 0,8 i ^ = - 0,18 ω B C   i ^ +   0,1 ω A B   i ^

- 0,6 j ^ = - 0,24 ω A B j ^

Resolvendo o sistema, encontramos o resultado final:

ω A B = 2,5   r a d / s

ω B C = 5,83   r a d / s

Resposta

ω A B = 2,5   r a d / s

ω B C = 5,83   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade angular ω do aríete AE do triturador de pedras na posição em que θ = 60 ° . A manivela OB possui uma taxa de velocidade angular de 60 rpm. Quando B está na parte mais baixa do s
O eixo em O conduz o braço AO a uma velocidade no sentido horário de 90 rpm em torno do mancal fixo em O. Utiliza o método do centro instantâneo de velocidade nula para determinar a velocidade de rota
No projeto desse mecanismo, o movimento ascendente do êmbolo G controla o movimento de uma vara de controle presa em A. O ponto B da haste AH está confinado a se deslocar com o curso deslizante sobre
9. Quando apenas duas engrenagens estão engrenadas, a engrenagem motriz A e a engrenagem movida B girarão sempre em direções opostas. A fim de fazer com que elas girem na mesma direção, uma engrenagem
29. A engrenagem A gira com uma velocidade angular constante ω A = 6 r a d s . Determine a maior velocidade angular da engrenagem B e a velocidade no ponto C.