Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 83
O volante gira no sentido horário com uma velocidade constante de 600 rpm, e a barra AB desliza através do cursor articulado em C. Para a posição , determina a velocidade angular de AB utilizando as relações de velocidade relativa. (Sugestão: Escolha um ponto D sobre AB coincidente com C como um ponto de referência cuja direção da velocidade é conhecida)
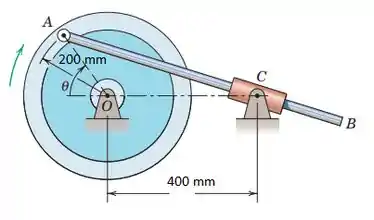
Passo 1
Inicialmente, o problema pode parecer muito complicado por misturar movimento circular com movimento linear.
Então, vamos escrever os dados de uma forma mais fácil de entender e converter para o SI:
- Vamos chamar a velocidade angular do volante de e passar para a unidade rad/s:
- O ponto A, por estar fixo ao volante, apresenta velocidade linear perpendicular ao vetor que passa pelo centro AO e pode ser calculada por:
- Vamos usar a recomendação do enunciado e criar um ponto D na barra, coincidente ao ponto C. Por estar situado na articulação C neste instante, o ponto D possui velocidade ( na direção de deslizamento da barra AB.
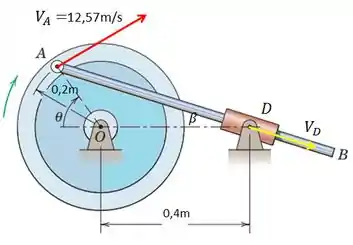
Passo 2
Antes de ir pra etapa de aplicação dos conceitos de velocidade relativa, é importante estabelecer algumas relações geométricas do triângulo ADO, de modo a encontrar o ângulo e o comprimento de AD.
Para isto, prolongamos os segmentos em O e em A, formando um triângulo retângulo.
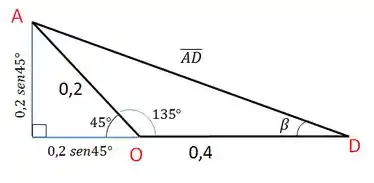
Desta forma, encontramos que:
e
Esta etapa é importante porque estes valores serão utilizados nos cálculos de velocidade relativa. Calma aí, já tá chegando.
Passo 3
Finalmente, vamos utilizar a tão esperada velocidade relativa!
E como queremos saber a velocidade angular da barra AB, vamos usar as velocidades dos pontos desta barra como referência, ou seja, A e D. Portanto:
Agora vem o grande pulo da questão: representar os gráficos dos vetores. Como vimos acima que o ponto D coincide com a articulação C neste instante, o movimento deste ponto tem a mesma direção da barra AB. E, como o vetor da velocidade relativa é perpendicular à barra, ele também vai ser perpendicular ao vetor velocidade . Vamos ilustrar pra ficar mais fácil.
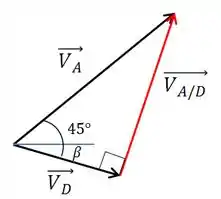
Agora, devemos somar os ângulos de e ,fazer uma simples relação de triângulo retângulo para determinar :
Por último, encontramos a velocidade angular da barra AB:
Demorou, mas saiu!