Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 84

Determine a velocidade angular ω da haste telescópica AB no instante representado. A velocidade angular de cada uma das barras de acionamento direto é indicada.

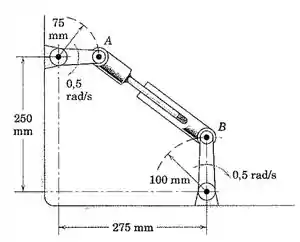
Passo 1

Nesta questão, temos as duas extremidades da haste telescópica presas a barras articuladas, onde ω A = ω B = 0,5 r a d / s . Sabendo os comprimentos e as velocidades angulares das barras, podemos determinar as velocidades lineares dos pontos A e B, que são perpendiculares à barra. Então, o vetor V A → vai estar na vertical apontando para baixo e o vetor   V B → vai estar na horizontal para direita.

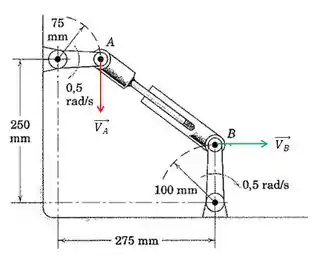
Ah, um detalhe muito importante: a haste telescópica AB é livre para aumentar ou diminuir o comprimento, portanto não se deve resolver esta questão pelo método de Centro Instantâneo de Velocidade.

Então, uma maneira simples de encontrar o ω da haste é usar o conceito de velocidade relativa para determinar primeiro o vetor velocidade ω A / B .

Passo 2

Vamos iniciar o desenvolvimento!

Primeiro, calculamos as velocidades V A   e   V B .

V A → = ω A × r A = 0,5 × 0,075 = 0,0375 m s ; s e n t i d o   h o r á r i o

V B → = ω B × r B = 0,5 × 0,1 = 0,05 m s ; s e n t i d o   h o r á r i o

Agora, vamos calcular o comprimento da haste neste instante, através de um simples Pitágoras:

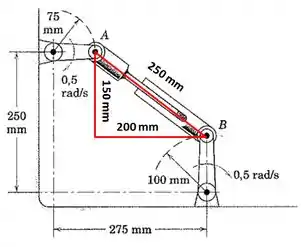
Passo 3

Nesta etapa vamos aplicar o conceito de velocidade relativa!

Sabemos que: V A → = V B → + V A B → , que pode ser representado vetorialmente juntando os dois vetores A e B, da seguinte forma:

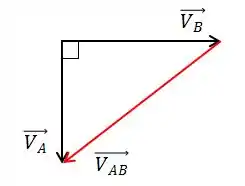
Portanto, usamos Pitágoras de novo, e encontramos V A B → = 0,0625   m / s .

Por fim, usamos a relação:

ω = V A B → A B - = 0,0625 0,25 = 0,25 r a d s ; s e n t i d o   A H

Resposta

ω = 0,25   r a d / s ; sentido anti-horário

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/118) A tira flexível está presa em E ao setor rotativo e passa sobre a polia guia . Determine as velocidades angulares de A D e B D para a posição apresentada se a tira tem uma velocidade de 4 m / s
5/112) A barra O A possui uma velocidade angular no sentido anti-horário θ ' = 4r a d / s durante um intervalo de seu movimento . Determine a velocidade angular da barra A B e do setor B D para θ = 45
5/115) Um dispositivo que testa a resistência ao desgaste de dois materiais A e B é apresentado . Se a barra E O possui uma velocidade de 1,2m / s para a direita quando θ = 45 ° , determine a velocida
5/113) O cilindro hidráulico produz um movimento horizontal limitado do ponto A . Se v A = 4m / s quando θ = 45 ° , determine o módulo da velocidade de D e da velocidade angular ω de A B D para essa p
Para o instante representado, o elemento D gira com uma velocidade angular ω = 2r a d / s e sua ranhura está vertical. Também nesse instante, θ = 60 ° . Determine a velocidade da extremidade A da barr